今回はpandasチュートリアルの四回目になっています。
前回のがまだという方は↓の記事を参照ください。
【python】データ分析のための「pandas」の使い方③:データフレームのフィルタリング
今回はデータフレームの統計量の求め方を学んでいきましょう!
全てサンプルコードを記載してあります。各々のpythonの環境で実際に手を動かしながら読み進めていってください。
サクッとやりたい方は、google colaboratoryが簡単でおすすめです。
統計量とは?
まずそもそも統計量とは何なのか?その説明からしますね。
統計量とは、データセットから得られる情報の要約で、平均、中央値、標準偏差、相関係数などが一般的な例です。
これらの統計量は、データセット全体の特徴を把握するのに役立ちます。
pythonで求められる統計量
pythonではサクッと様々な統計量を求める事ができます。
以下が代表的なものです。
- mean() : 平均値を求める。
- median() : 中央値を求める。
- mode() : 最頻値を求める。
- std() : 標準偏差を求める。
- var() : 分散を求める。
- min() : 最小値を求める。
- max() : 最大値を求める。
- sum() : 合計値を求める。
- count() : データ数を求める。
多いですが、どれも簡単ですのでひとつずつ見ていきましょう。
データ準備
ではまずデータセットの準備をしましょう。
いままでは’iris’のデータセットを使っていましたが、今回は’tips’というあるレストランの売上とチップをまとめたデータを使いましょう。
|
1 2 3 4 5 |
import pandas as pd import seaborn as sns df = sns.load_dataset('tips') df |
これで’tips’のデータフレームができました。
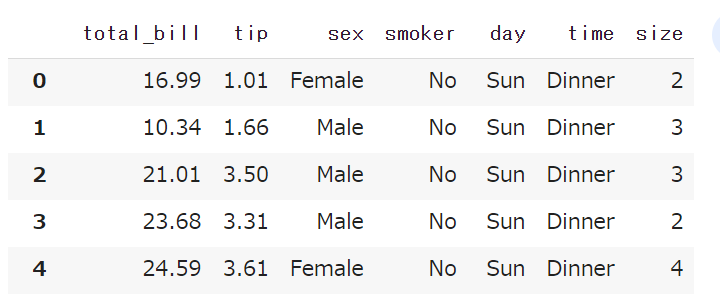
分かりやすいデータフレームですね。
各カラムの詳細を記載します。
- total_bill:お会計の合計金額(ドル)
- tip:チップの金額(ドル)
- sex:支払いをした人の性別(男性または女性)
- smoker:禁煙者かどうか(YesまたはNo)
- day:支払いをした曜日(Thur、Fri、Sat、Sunのいずれか)
- time:支払いをした時間帯(LunchまたはDinner)
- size:支払いをしたグループの人数
pythonで統計量を求めてみよう
では実際にpythonで統計量を求める方法を見ていきましょう。
平均値を求める
まずは平均値です。これは説明の必要もないですね。
mean()ですぐに求められます。
|
1 2 |
# 平均値 df.mean() |
->
total_bill 19.785943
tip 2.998279
size 2.569672
このようにデータフレーム全体にmean()すると、数値型のカラムだけ自動で平均値を求めてくれます。
もちろんカラムを絞って求める事もできます。
|
1 2 |
# tipカラムの平均値 df['tip'].mean() |
-> 2.99827868852459
中央値を求める
中央値は、データセットの値を小さい順に並べたときに中央に位置する値のことを指します。つまり、データセットの中央に位置する値です。
中央値は平均値とは異なり、外れ値の影響を受けにくいのが嬉しいポイントです。
median()を使う事で求められます。
|
1 2 |
# 中央値 df.median() |
->
total_bill 17.795
tip 2.900
size 2.000
平均値と中央値を比べると変わりますね~、特にtotal_billの値が2ドル位変わります。
外れ値の影響ですね。
もちろん、カラムを指定して求める事もできます。
|
1 |
df['tip'].median() |
->tip 2.900
最頻値を求める
最頻値とは、ある集合やデータの中で、最も頻繁に出現する値のことを指します。
mode()で求めることができます。
|
1 2 |
# 最頻値 df.mode() |
最頻値の場合は数値型だけでなく、文字列に対しても実行されます。
カテゴリーなどに対して、一番出てくるカテゴリーを表示してくれます。
標準偏差を求める(不偏標準偏差)
標準偏差とは、データのばらつき具合を表す指標のひとつで、平均値からの偏差の2乗和の平均値の平方根です。
つまり、各データの平均値からの距離が大きいほど、標準偏差は大きくなります。
標準偏差が大きいほど、データのばらつきが大きいことを示し、標準偏差が小さいほど、データのばらつきが小さいことを示しています。
標準偏差は、数式で以下のように表されます。
$$\sigma = \sqrt{\frac{1}{N-1}\sum_{i=1}^N(x_i – \mu)^2}$$
ここで、$\sigma$は標準偏差、$n$はデータ数、$x_i$は$i$番目のデータ、$\mu$は平均値を表します。
pythonではstd()で表せます。
|
1 2 |
# 標準偏差 df.std() |
->
total_bill 8.902412
tip 1.383638
size 0.951100
分散を求める(不変分散)
分散は標準偏差と算出方法が似ており、ルートをしないだけの違いになります。
そのため、単位が元の単位と揃わないので、直感的に分かり辛いです。(平均身長の分散が60と出ても、そのまま60cmと捉える事ができない。)
$$\sigma^2 = \frac{1}{N-1} \sum_{i=1}^{N} (x_i – \mu)^2$$
分散は上記の式で表す事が出来、標準偏差の式からルートを無くしただけです。
分散は$\sigma^2$で表します。
|
1 2 |
# 分散 df.var() |
->
total_bill 79.252939
tip 1.914455
size 0.904591
最大値と最小値を求める
それぞれのカラムに入っている値の最大値と最小値も求める事ができます。
最大値はmax()で、最小値はmin()を使います。
|
1 2 |
# 最大値 df.max() |
->
total_bill 50.81
tip 10.00
size 6.00
|
1 2 |
# 最小値 df.min() |
->
total_bill 3.07
tip 1.00
size 1.00
結果をみると、合計金額(total_bill)は3ドル~50ドルの間に収まっている事がわかりますね。
合計を求める
それぞれのカラム毎の合計値を求めてみましょう。
sum()を使えば一発です。
|
1 2 |
# 合計 df.sum() |
->
total_bill 4827.77
tip 731.58
size 627.00
データ数を求める
カラムの何個データが入っているのか?を求めるにはcount()を使います。
|
1 2 |
# データ数を求める df.count() |
->
total_bill 244
tip 244
sex 244
smoker 244
day 244
time 244
size 244
全て244になっていますね。count()も数値型だけでなく、文字列の値も返してくれます。
また欠損値があった場合には、それはカウントしないので注意してください。
‘tips’のデータセットには欠損値がないので、わざと欠損値のあるデータフレームを作って見てみましょう。
|
1 2 3 4 5 6 7 8 |
# 欠損値のあるデータを作成 data = {'A': [1, 2, None, 4, 5], 'B': [None, 2, 3, 4, 5], 'C': [1, 2, 3, 4, 5]} df_nan = pd.DataFrame(data) df_nan.count() |
->
A 4
B 4
C 5
この様に、欠損値のあるAとBは数が4になっています。
おさらい:describeとcorr
第二回目のチュートリアルでもやった以下の2つも覚えているでしょうか?
データサイエンスに必須の関数ですね
- describe()
- corr()
覚えてないって方は【python】データ分析のための「pandas」の使い方②:データフレームの中を見よう!を見て見てください。
簡単にだけ説明します。
describe()
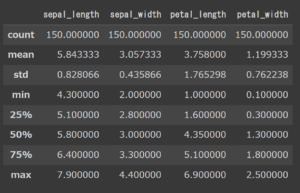
describe()はpandasデータフレームの統計情報を計算して表示するための便利なメソッドです。
|
1 |
df.describe() |
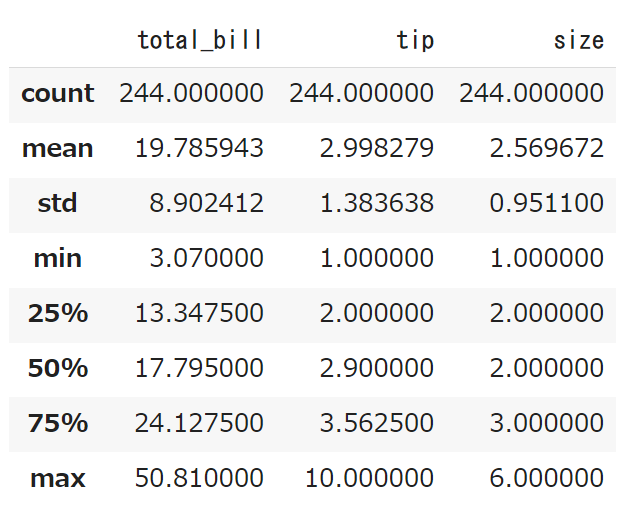
corr()
corr()数値型の列同士の相関係数を全てパッと出してくれます。
ちなみに相関係数を簡単に説明すると、2つの変数間の関係の強さを数値で表す統計指標の一つです。
具体的には、2つの変数がどの程度同時に変化するかを表現します。
相関係数は、-1から1までの値を取り、絶対値が1に近いほど2つの変数は強い相関があるといえます。
|
1 |
df.corr() |
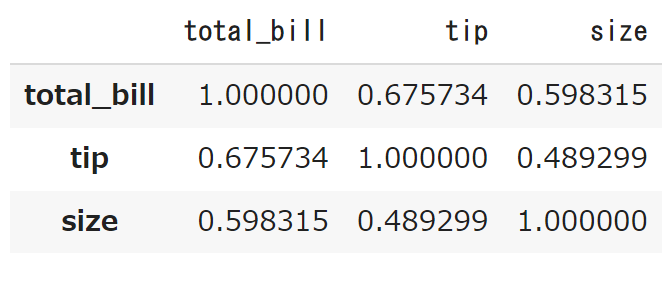
対角線上は同じカラム同士の相関なので、1になっています。
まとめ
いかがでしたでしょうか?
色々な求め方が出てきたので、なかなか一回では覚えられないと思います。
なんども使ってみて、自分の物にしていきましょう!
特にdescribe()やcorr()は、新しいデータセットに触れる際は必ずと言って良いほど使いますし、何かとmean()で平均値を求める事も多いです。
ここら辺が出来ると大分データサイエンスっぽくなってきますね!













