今回はpythonで良く出てくるnumpyって一体何なのか?
どんな時につかうの?データ分析で必要なの?
この様な悩みにお答えします。
データサイエンスをやるならnumpyは必須です。
特に機械学習で真価を発揮しますので、まずはどういった物かを理解しましょう。
ちなみにこの後サンプルコードも出てきますので、ハンズオンでやりたいという方で、サクッとpythonを動かしたい方は、google colaboratoryが簡単でおすすめです。
numpyとは?
「numpy」とは、Python言語の数値計算ライブラリであり、大規模な多次元配列や行列の処理を高速化するための関数やメソッドが提供されています。
また、線形代数、統計学、フーリエ変換、乱数生成、フィルタリング、最適化などの数学的処理をサポートしています。
数多くの科学技術分野やデータサイエンス、機械学習、人工知能などでも使用されており、Pythonで数値計算を行う際には欠かせないライブラリとなっています。
numpyの具体的な機能
具体的には、numpyは以下のような機能を提供しています。
- 高速な数値計算:numpyはC言語やFortranで書かれたライブラリを内部的に使用し、多次元配列や行列の計算を高速化しています。
- 多次元配列のサポート:numpyはn次元配列をサポートしており、このために多次元配列に関する操作が非常に簡単に行えます。
- 高度な数学関数の提供:numpyは三角関数、指数関数、対数関数など、様々な高度な数学関数を提供しています。
- 行列演算:numpyは線形代数に必要な行列の演算をサポートしています。
numpyの使い方
NumPyの使い方は簡単で、まずはNumPyをインストールしてから、import文でNumPyを呼び出します。
次に、NumPyの配列を作成するには、numpy.array()関数を使用します。これにより、Pythonのリストをndarrayに変換できます。
ndarrayとは?
ndarrayという言葉を初めて聞いた人も多いと思います。
ndarray(N-dimensional array)とは、多次元配列(行列)を効率的に扱うためのデータ型のことです。
ndarrayは、スカラー、ベクトル、行列、立方体などのn次元配列を作成することができます。
NumPyの最も重要な機能の一つは、ndarrayを使用したベクトルおよび行列演算が高速に処理されることです。
ndarrayは、Pythonの標準リストよりも多くのデータを扱うことができ、大量の数値データを高速に処理できることが特徴です。
また、ndarrayは、Pythonのリストよりも多くの数学関数をサポートしているため、科学技術計算に適したデータ型と言えます。
つまり、ndarrayとは下記の特長をもっています。
- データ型のひとつ
- 行列の計算を高速に行う事ができる
- 平均や分散を求める数学系の関数をサポートしている
行列を作ってみよう
ではせっかくなので、numpyで行列をつくり、行列同士の計算を見てみましょう。
より理解が深まると思います。
まずは2つの行列を作ってみます。
numpyのインポートからのコードを書いてみます。
|
1 2 3 4 5 |
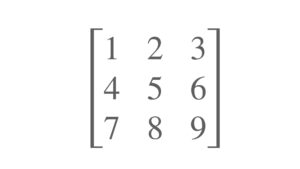
import numpy as np # 3×3の行列を作成 A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) B = np.array([[9, 8, 7], [6, 5, 4], [3, 2, 1]]) |

無事AとBの行列ができました。
行列同士の足し算
次に行列同士の足し算を見てみましょう。
|
1 2 3 4 |
# 行列の足し算 C = A + B print("A + B = ") print(C) |

無事に足し算をすることができました。
行列の掛け算
続いて掛け算です。
やり方を覚えていますか?久しぶりだと忘れてしまいますよねw
|
1 2 3 4 |
# 行列の積 C = A.dot(B) print("A × B = ") print(C) |

このように、numpyを使う事で、簡単に行列同士の計算を行う事ができます。
numpyの重要な機能
numpyには他に重要な機能として、以下の物があります。
- 配列操作
- ブロードキャスト
- 乱数生成
配列操作とは?
配列操作は、NumPyを使用する上で最も頻繁に使用される機能の一つです。
配列操作には、配列の形状、次元数、軸の順序を変更する機能が含まれます。
また、配列の一部を切り出したり、軸を追加したり、削除したりすることもできます。
例えばですが、1次元の配列を2次元に変換する事もでます。
|
1 2 3 4 5 |
# 1次元配列の作成 arr1d = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]) # 2次元配列に変換 arr2d = arr1d.reshape((3, 3)) |
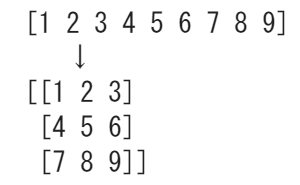
1次元の配列が、3×3の2次元の配列に変換されました。
このように、配列操作では変換したり、配列の一部を切り出したり、軸を追加したり、削除したりすることもできます。
ブロードキャストとは?
ブロードキャスト(broadcast)は、異なる形状の配列間の演算を可能にするものです。
通常、異なる形状の配列を演算するためには、それぞれの配列の形状を合わせる必要がありますが、ブロードキャストを使用すると、配列の形状を合わせずに演算を行うことができます。
例えばですが、以下の1列3行と3列1行の配列が違う形状の行列があります。
\begin{pmatrix}
1 \\
2 \\
3
\end{pmatrix}
\begin{pmatrix}
1 & 2 & 3
\end{pmatrix}
これを何か特殊な事をせずとも、うまい具合に足し算してくれるのです。
コードも非常にシンプルです。
|
1 2 3 4 5 6 7 8 9 |
# 配列の定義 a = np.array([1, 2, 3]) b = np.array([[1], [2], [3]]) # ブロードキャストを使用した演算 c = a + b # 結果の出力 print(c) |
\begin{pmatrix}
2 & 3 & 4\\
3 & 4 & 5\\
4 & 5 & 6
\end{pmatrix}
このように、自動で3×3の行列ができました。
乱数生成
NumPyには様々な種類の乱数生成関数があります。
これらの関数は多くの場合、シミュレーションやランダムなデータの生成に用いられます。たとえば、機械学習においては、データの前処理においてランダムなノイズを加えることがあります。
また、金融工学においては、モンテカルロシミュレーションによる価格の予測に用いられることがあります。
NumPyの乱数生成機能は、これらの分野での応用に幅広く活用されています。
代表的な乱数生成関数には、以下のものがあります。
- rand():0から1までの一様分布で乱数を生成
- randint():指定した範囲内の整数の乱数を生成
- randn():標準正規分布で乱数を生成
- normal():任意の平均値と標準偏差を持つ正規分布で乱数を生成
- uniform():指定した範囲内の一様分布で乱数を生成
numpyの応用例
更にnumpyを深堀りしていくと、様々なビジネスシーンにおいても非常に重要な役割を持っています。
特に代表的なのが以下の2つです。
- 画像処理
- 機械学習
画像処理におけるnumpy
NumPyは、画像処理やコンピュータビジョンの分野で広く使用されています。
画像は通常、ピクセル値の配列として表され、NumPy配列として扱うことができます。NumPyを使用すると、画像処理に必要な様々な機能を実装することができます。
さらに、NumPyは、画像フィルタリング、エッジ検出、形状認識などの高度な画像処理アルゴリズムの実装にも利用されます。
例えば、畳み込み演算を使用して画像フィルタリングを行うことができます。
NumPyを使用した画像処理の実装には、OpenCVやPillowなどのライブラリと組み合わせることが一般的です。
総じて、NumPyは、画像処理の分野において、高速で効率的なデータ処理と多くの機能を提供することで、重要な役割を果たしています。
機械学習におけるnumpy
機械学習におけるNumPyの応用例は、データセットの読み込み、前処理、特徴量エンジニアリング、モデルの学習、評価などです。
例えば、データセットをNumPy配列として読み込んで、欠損値を補完したり、カテゴリ変数を数値に変換する前処理を行うことができます。
さらに、NumPyを使用して、機械学習モデルの学習や評価を行うことができます。
例えば、線形回帰やロジスティック回帰のような単純なモデルから、ニューラルネットワークやランダムフォレストのような複雑なモデルまで、NumPyを使用して実装することができます。
総じて、NumPyは機械学習において欠かせないライブラリの1つです。
まとめ
いかがでしたでしょうか?
numpyはデータサイエンスをやる上で必須になってきます。
- 行列演算を行う
- 配列を操作する
- 機械学習に活用する
この様な重要な機能があります。
今回説明したもの以外にもたくさんの機能がありますので、ゆっくり覚えていきましょう。
これからもnumpyに関する講義を行っていきますので、そちらもご覧ください。
ちなみにpandasについても知りたい方は下記の記事をどうぞ!
【python】データ分析のためのpandasの使い方①:データフレームの作成
使用したイラストは↓コチラです。
Work illustrations by Storyset















