この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 分散って何?
- 偏差値はどうやって計算してるの?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回は統計学、、いや生きていくうえで絶対に必要な「分散」と「標準偏差」について解説します。
「言い過ぎだよ~!」っと思うかも知れませんが、本当にその位大事な内容になっています。
これを理解せずして統計検定に合格する事は絶対にできません。
ではさっそく講義を始めていきましょう!
分散とは?
分散や標準偏差とは、一言で言うと↓の通りです。
データのばらつき具合を表す統計量です。
分散はデータが平均値からどれだけ離れているかを測定するものです。
分散が大きいということは、データが平均値から離れていることが多いことを意味し、分散が小さいということは、データが平均値に集中していることを意味します。
例えば、以下の2つのデータセットがあります。
この2つの平均は50.5で一緒です。
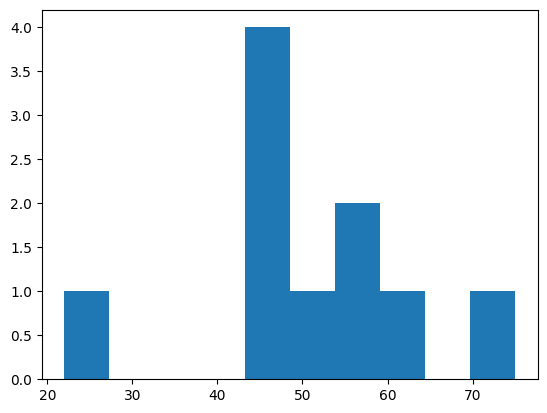
- A:$[45, 48, 59, 44, 60, 22, 44, 56, 75, 52]$
- B:$[49.7, 50.3, 49.8, 50.2, 49.9, 50.1, 49.6, 50.4, 50, 50.5]$
しかし、ヒストグラムで見て見ると、データの散らばり具合が全く違う事がわかります。
Aのデータセット
Bのデータセット
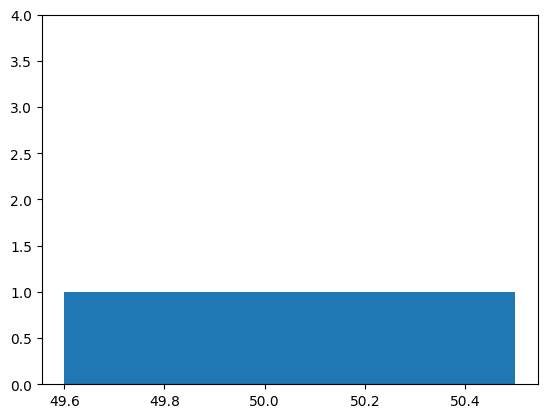
平均値は一緒でも全く違う形のヒストグラムになりましたね!
このように、データの平均だけでは分からないデータの散らばり具合を表す指標の一つが分散なのです。
分散の求め方
では実際に分散の求め方を見ていきましょう。
分散の公式
分散を求める公式は↓です。
$\frac{\sum_i (x_i – \bar{x})^2}{n}$
もう一度記号の意味を確認しておきましょう。
- $x_i$:データポイント
- $\bar{x}$:データの平均
- $n$:データポイントの数
分散を求めてみよう
分散を求めるには先ほどの公式に当てはめましょう。
流れとしてはコチラです。
- $\bar{x}$(平均)を求める
- データポイント毎の偏差を求め二乗する
- 偏差の二乗を全て足し合わせる
- データポイントの数で割る
では実際に↓のサンプルデータで分散を求めてみましょう。
$[45, 50, 43, 62, 56, 52, 39, 53]$
まずは$\bar{x}$(平均)を求めましょう。
$(45+50+43+62+56+52+39+53)/8 = 50$
平均が$50$だと分かりました。
データポイント毎の偏差を求め二乗する
公式だと$(x_i – \bar{x})^2$この部分ですね。
$x_i$にデータポイントが次々に入っていきます。
また、偏差という単語の説明ですが、各データポイントから平均を引いた値が偏差です。$(x-\bar{x})$この部分の結果です。
上のサンプルデータの場合、$45-50 = -5$、$50-50 = 0$,,,,,と各偏差を求められます。
そして、偏差を全て二乗します。
↓が各データポイントの偏差とその二乗をまとめたものです。
| データ | 45 | 50 | 43 | 62 | 56 | 52 | 39 | 53 |
| 偏差 | -5 | 0 | -7 | 12 | 6 | 2 | -11 | 3 |
| 二乗 | 25 | 0 | 49 | 144 | 36 | 4 | 121 | 9 |
全て足し合わせデータポイントの数で割る
そして、$\sum_i$この記号が示す意味の、偏差の二乗を全て足し合わせ、その後にデータポイントの数(今回は8)で割ります。
そうする事で分散を求める事ができます。
$(25+0+49+144+36+4+121+9)/8=48.5$
分散:48.5という結果で導きだせました。
なぜ偏差を二乗するのか?
補足として、偏差を二乗するのには意味があります。
分散はデータのバラつきを表す事は最初にお伝えした通りです。
要は、平均から各データポイントまでの距離(偏差)がどれだけ離れているのか?を足し合わせたのが分散の正体です。
そのため、ただの偏差だと正の値もあれば、負の値もありますし、そもそも足し合わせると必ず0になってしまいます。
ですので、二乗する事で全ての偏差を正の値にし、それらを足し合わせる事で正しく平均からどれだけ距離が離れているのかを確認する事ができるのです。
もう一つの分散の公式
実は分散の公式にはもう一つあります。
検定ではこちらの公式で出題される事もあるので、覚えておきましょう。
$s^2=\overline{x^2}-(\bar{x})^2$
記号の意味としては↓です。
- $s^2$:分散。$\sigma$(シグマ)で表す事もあります。
- $\overline{x^2}$:各データポイントの二乗の平均
- $(\bar{x})^2$:平均の二乗
つまり、データポイントの二乗の平均を求めてから、平均の二乗を引けば分散を求められるのです。
式の証明
では先ほどのデータを基に、分散を求めてみましょう。
平均は50で分かっているので、まずはデータの二乗を計算します。
| データ | 45 | 50 | 43 | 62 | 56 | 52 | 39 | 53 |
| 二乗 | 2025 | 2500 | 1849 | 3844 | 3136 | 2704 | 1521 | 2809 |
次に、この二乗の平均を求めてから、平均の二乗を引いて分散を求めます。
$\frac{2025 + 2500 + 1849 + 3844 + 3136 + 2704 + 1521 + 2809}{8}-(50)^2$
$= 2548.5 – 2500 = 48.5$
結果、分散が$48.5$という事で、初めの公式で求めた分散と同じ結果になりました。
標準偏差とは?
分散のデメリットとして、単位が分かり辛いというのがあります。
- 平均:50
- 分散:48.5
この数値を見ても平均に対してどれくらいデータが散ら買っているのか分かり辛いですよね?
平均50に対して、48.5の範囲でズレがあるというわけではありません。
二乗しているために、分かり辛くなっています。
そんな時に使うのが標準偏差です。
標準偏差の公式
まず標準偏差の公式は↓です。
$s = \sqrt{\frac{\sum_i (x_i – \bar{x})^2}{n}}$
気づいたでしょうか?
そう、分散の公式にルートが付いただけなのです。
標準偏差の求め方
簡単ですね、分散の正の平方根を求めれば良いのです。
先ほどの分散48.5の標準偏差を求めるには↓のようにすればOKです。
$s = \sqrt{48.5} =6.96…$
標準偏差は6.96という事が分かりました。
これは個々のデータポイントと平均値との距離が、平均すると6.96ある事を示しています。
データの合算
統計検定の試験では、以下の様な問題もでてきます。
A組とB組のテストの結果、A組は分散が625、B組は121でした。
クラスメイトの数は両クラスとも20名で、平均点は60点でした。
A組とB組を合わせたデータの分散はいくつか?
さっそく解いてみましょう。
分散の公式を使う
$s^2=\overline{x^2}-(\bar{x})^2$
この公式を使いましょう。この式は、
$分散=\frac{データの二乗和}{データ個数} – 平均の二乗$
ですので、各値を代入できそうですね。
データ個数と平均の二乗、分散は問題文に書いてあるので、データの二乗和が分かればなんとか解けそうですね。あとやる事は、
- 各クラスのデータの二乗和を求める
- データを合算して分散を求める
これだけです。やってみましょう!
各クラスのデータの二乗和を求める
まずはA組の二乗和を求めます。公式に代入しましょう。
$\frac{A^2}{20}-60^2=625$
$\frac{A^2}{20}=625 + 60^2$
$\frac{A^2}{20}=4225$
$A^2=4225 ×20 = 84500$
A組の二乗和は84500でした。
では続いてB組を求めます。
$\frac{B^2}{20}-60^2=121$
$\frac{B^2}{20}=121 + 60^2$
$\frac{B^2}{20}=3721$
$B^2=3721 ×20 = 74420$
B組も分かりました。
では合算して分散を求めましょう!
出そろったデータを合算しつつこの公式に当てはめます。
$分散 = \frac{データの二乗和}{データ個数} – 平均の二乗$
$AB^2 = \frac{A^2 + B^2}{20 + 20} – 60^2$
$AB^2 = \frac{84500 + 74420}{40} – 3600$
$AB^2 = 373$
この様にして求める事ができます。
注意点として、今回は2クラスの平均点が50点と一緒だったために、$50^2$として使えました。
しかし、もしこの値が違った場合は、前にやった加重平均を使って再度合算の平均点を求める必要があります。
加重平均に関しては↓の講座をご覧ください。

変動係数
変動係数は数値の範囲が大きが違うもののデータのバラつきを比較する時に重要になってくる値です。
例えば、あるお寿司屋さんの大トロと赤身の値段の平均と標準偏差が↓の場合を見てみましょう!
| 平均価格 | 標準偏差 | |
| 大トロ | 2000 | 4000 |
| 赤身 | 400 | 1000 |
パッと見では大トロの方が分散の数値が大きいので、データのバラつきが大きい様に感じますよね?
しかし、平均価格が5倍以上の差があるので、単純に分散や標準偏差の数値だけを見てデータのバラつきの優劣を付ける事ができないのです。
そんな時に大事なのが変動係数です。
変動係数の求め方
$CV = \frac{\sigma}{\bar{x}}$
この公式を使います。
今回は標準偏差($s^2$)を$\sigma$で表しています。
まずは大トロの変動係数を求めます。
$CV = \frac{4000}{2000}$
$CV = 2$
続いて赤身を求めます。
$CV = \frac{1000}{400}$
$CV = 2.5$
この様な結果になりました。
大トロが2で赤身が2.5のため、実は赤身の方がバラつきがあるという驚きの結果になりました。
分布の変形
変動係数もそうでしたが、異なる分布を比較するもう一つの方法があります。それが、
分布を変形して平均や分散を揃えて比較する方法です。
どういう事かと言うと、ある学校のテスト結果が↓です。
| 平均点 | 分散 | |
| 英語 | 63 | 144 |
| 数学 | 82 | 361 |
このように、点数の分布が違うと両者の点数を単純に比較する事が出来ないのです。
例えばA君が英語で70点、数学で78点を取ったとします。
これだけ見ると、A君は数学の方が得意に見えますが実際には平均点が大きく違い、平均点以上に点数を取っているのは英語です。
この様な時に、平均点や分散を揃えて比較する事で、A君の実力を確実に把握する事ができるのです。
このやり方も見ていきましょう。
分布の形を変えるには?
まず覚えておいて欲しい点があります。
各データポイントに値$a$を加えると、平均$\bar{x} + a$になるが、分散は変化しません。
例えば、以下のデータセットを見てみましょう!
$[4, 5, 2, 3, 4]$
これの平均と分散を求めます。
平均は単純に計算すると3.6ですね!次に分散を求めます。
$s^2 = \frac{(4 – 3.6)^2 + (5 – 3.6)^2 + (2 – 3.6)^2 + (3 – 3.6)^2 + (4 – 3.6)^2}{5}= 1.04$
- 平均:3.6
- 分散:1.04
次はこのデータセットの各値に3を加えた結果の平均と分散を見てみましょう!
| 4 | 5 | 2 | 3 | 4 |
| 7 | 8 | 5 | 6 | 7 |
$\bar{x} = \frac{7+8+5+6+7}{5}= 6.6$
続いて分散を求めます。
$s^2 = \frac{(7 – 6.6)^2 + (8 – 6.6)^2 + (5 – 6.6)^2 + (6 – 6.6)^2 + (7 – 6.6)^2}{5}= 1.04$
- 平均:6.6
- 分散:1.04
この様な結果となりました。
全データポイントに3を足すと、平均は3増えるが分散は変わらないという事がわかりましたね。
もちろん、逆に3を引いた場合ですと、平均は3減りますが分散は変わりません。
k倍するとどうなるか?
では続いてk倍した場合の変化を見てみましょう。
基本的には以下の通りです。
- $k$倍すると、平均は$k$倍になり分散は$k^2$倍になる。
- $\frac{1}{k}$倍すると平均は$\frac{1}{k}$倍になり分散は$\frac{1}{k^2}$になる。
では先ほどのデータセットを2倍した場合を見てみましょう。
$[4, 5, 2, 3, 4]$→$[8, 10, 4, 6, 8]$
まずは平均を求めます。
$\bar{x} = \frac{8+10+4+6+8}{5}= 7.2$
次に分散を求めます。
$s^2 = \frac{(8 – 7.2)^2 + (10 – 7.2)^2 + (4 – 7.2)^2 + (6 – 7.2)^2 + (8 – 7.2)^2}{5}= 4.16$
- 平均:$7.2$
- 分散:$4.16$
この様な結果になりました。
先ほどのと比べてみましょう。
平均は$k$倍(今回は$2$倍)で分散は$k^2$倍するんでしたね。
- 平均:$3.6×2=7.2$
- 分散:$1.04×2^2=1.04×4=4.16$
うん、あってますね!
標準化しよう
新しい単語として標準化が出てきました。この意味は、
平均0、分散1の分布をつくる事です。
まず、なぜこんな事をするかと言うと、これをする事で先ほどから話しに出ている英語と数学のテストの結果のものさしを一緒にして、A君の実力を測る事が出来るからです。
これにも公式があります。
$z = \frac{x-\bar{x}}{s}$
ちなみに$z$はそのままz得点と言います。平均0、分散1の場合の各値の事です。
また$s$は標準偏差の事です。
z得点を求める流れは↓です。
- 各データから値$\bar{x}$を引く。この段階で平均は0になりますが分散は変化しません。
- 次に$\frac{1}{s}$倍する。これにより分散は$\frac{1}{s^2}$倍になり0になります。
簡単ですね。
各データから$\bar{x}$を引き、標準偏差で割ると平均0、分散1になるのです。
A君のz得点を求めよう
では実際にA君のz得点を求めましょう。
各平均値と分散は↓でしたね。
| 平均点 | 分散 | A君の得点 | |
| 英語 | 63 | 144 | 70 |
| 数学 | 82 | 361 | 78 |
まずは英語です。公式に当てはめます。
$z_1 = \frac{70-63}{\sqrt{144}}=0.58$
続いて数学です。
$z_2 = \frac{78-82}{\sqrt{361}}=-0.21$
この様な結果になりました。
英語は0.58で数学は-0.21という事で、英語の方がz得点が良いという事が分かりましたね!
偏差値を求める
偏差値は皆さん聞いた事ありますよね?
50を基準にその上下で一喜一憂する事も多いと思います。
実は、z得点を使えばすぐに偏差値を求める事が出来るのです。
それが以下の公式です。
$T = \frac{x-\bar{x}}{s}×10+50=z×10+50$
やっている事は非常に簡単ですね。
- z得点に10を掛ける
- 次に50を足す
ようは、平均が50で標準偏差が10(分散100)になるようにしています。
z得点は平均が0で分散が1でしたね。
z得点にまず10を掛ける事で平均0、分散が$10^2$倍で100になります。
そこに50を足せば、分散は変わらず平均が50になり、偏差値の完成です。
A君のテストの結果を偏差値で表してみましょう。
まず英語です。
$T = 0.58×10+50=55.8$
次に数学です。
$T = -0.21×10+50=47.9$
まとめると、
- 英語:55.8
- 数学:47.9
となり、A君は英語が得意だという事がわかりました。
練習問題
では最後に練習問題に取り組み、今回の内容を自分のものにしましょう。
標準偏差
$[4, 5, 2, 3, 7]$
答え:2.96
まずは平均を求めると、4.2になります。それを公式に当てはめます。
$s = \sqrt{\frac{(4-4.2)+(5-4.2)+(2-4.2)+(3-4.2)+(7-4.2)}{5}}=2.96$
データの合算
データAは平均50、分散540、データ個数は10個である。
データBは平均60、分散350、データ個数は15個である。
答え:平均56、分散450
まずは合算の平均を求めます。
次のように加重平均で計算します。
$\bar{x} = \frac{50×10+60×15}{25}=56$
次にデータのA、Bのデータの二乗和を求めます。
$\frac{A^2}{10}-50^2=540$
$A^2=(540+2500)×10 $
$A^2=30400 $
次にBです。
$\frac{B^2}{15}-60^2=350$
$B^2=(350+3600)×15 $
$B^2=59250 $
加重平均とAとBの二乗和を求める事ができたので、それを公式当てはめれば分散が出ます。
$S^2 = \frac{30400+59250}{10+15}-56^2=3586-3136=450$
変動係数
| 平均 | 標準偏差 | |
| A | 1200 | 6400 |
| B | 280 | 1950 |
答え:A.5.3 B.6.96
変動係数は標準偏差割る平均で求めます。
$A= \frac{6400}{1200}=5.3$
$B= \frac{1950}{280}=6.96$
偏差値
A君が数学のテストを受けた結果が↓です。
| A君の点数 | 平均点 | 分散 | |
| 数学 | 84 | 75 | 144 |
答え:57.5
z得点を求めてから10倍し、50を足せば良いんです。
$T = \frac{84-75}{\sqrt{144}}×10+50=\frac{9}{12}×10+50=57.5$

Work illustrations by Storyset