ローレンツ曲線とジニ係数【0から始める統計検定2級講座⑥】

この講座の対象者は以下の方を想定しています。

この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。

今回は見落としがちな、ローレンツ曲線とジニ係数について解説します。

 

 

ローレンツ曲線とは？

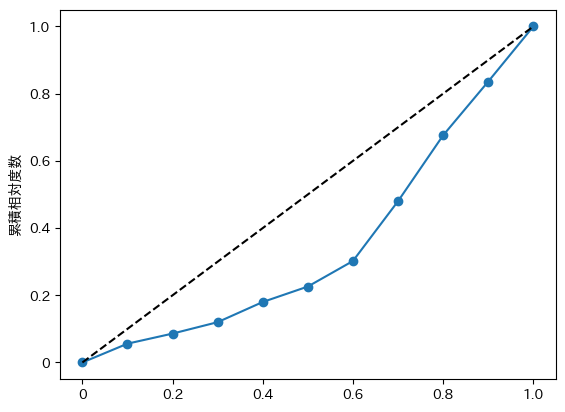
ローレンツ曲線は、1905年にアメリカの経済学者、マックス・O・ローレンツによって最初に開発されました。

人口の累積相対度数を横軸に、所得または富の累積相対度数を縦軸にとった折れ線グラフで、所得や富の分布の不平等を測定するために作られました。
完全平等の状態は、ローレンツ曲線が45度の線になります。ローレンツ曲線が45度の線から離れるほど、所得や富の分布は不平等になります。

統計では、富の不平等だけでなく、「偏り＝不均等さ」を表すために良く使われます。

 

 

ローレンツ曲線の作り方

ローレンツ曲線の作り方としては、↓の流れです。

この流れです。
では詳しく見ていきましょう。

 

 

今回使うデータセット

例えば、A社とB社の社員10人の給料をまとめたのが↓の表です。
2社とも10人の合計の金額は5000万です。
ローレンツ曲線を使えば、どちらの会社の方が公平かをすぐに調べる事ができます。

	1	2	3	4	5	6	7	8	9	10
A社	380	440	410	450	690	520	540	550	550	470
B社	280	320	400	530	480	820	740	800	300	330

 

データを昇順にし累積相対度数を出す

まずは、上記のデータを昇順にソートし、給与の相対度数と累積相対度数を出します。

累積相対度数とは、読んで字の如く相対度数を累積していく値です。
言葉で説明するよりも、↓の表の一番右の列を見る方が早いです。

 

A社

	給与	相対度数	累積相対度数
1	380	0.076	0.076
2	410	0.082	0.158
3	440	0.088	0.246
4	450	0.09	0.336
5	470	0.094	0.43
6	520	0.104	0.534
7	540	0.108	0.642
8	550	0.11	0.752
9	550	0.11	0.862
10	690	0.138	1
合計	5000	1	1

A社の累積相対度数が分かりましたね！
では続いてB社を求めてみましょう！

B社

	給与	相対度数	累積相対度数
1	280	0.056	0.056
2	300	0.06	0.116
3	320	0.064	0.18
4	330	0.066	0.246
5	400	0.08	0.326
6	480	0.096	0.422
7	530	0.106	0.528
8	740	0.148	0.676
9	800	0.16	0.836
10	820	0.164	1
合計	5000	1	1

無事A社とB社の累積相対度数を知る事ができましたね！

 

 

ローレンツ曲線のプロット

上記の結果をプロットしたのがコチラです。

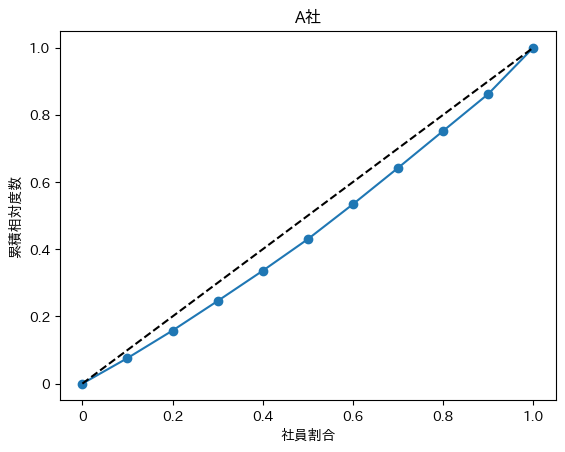
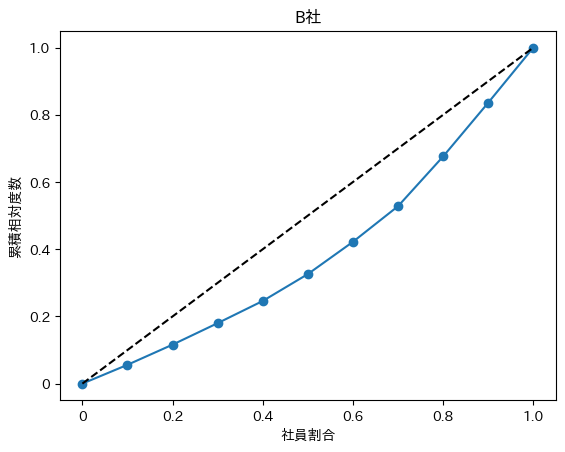
X軸は社員の割合を示しており、Y軸は累積相対度数を表しています。
また、線が2つあると思いますがその意味としては↓です。

 

 

ローレンツ曲線の見方

最初にローレンツ曲線は「不均等」さを表すとお伝えしました。
ではこの図からどのように読み取れば良いのかを解説します。
簡単に言うと、

完全平等線とローレンツ曲線の間にスペースがあるほど不均等です。

 

 

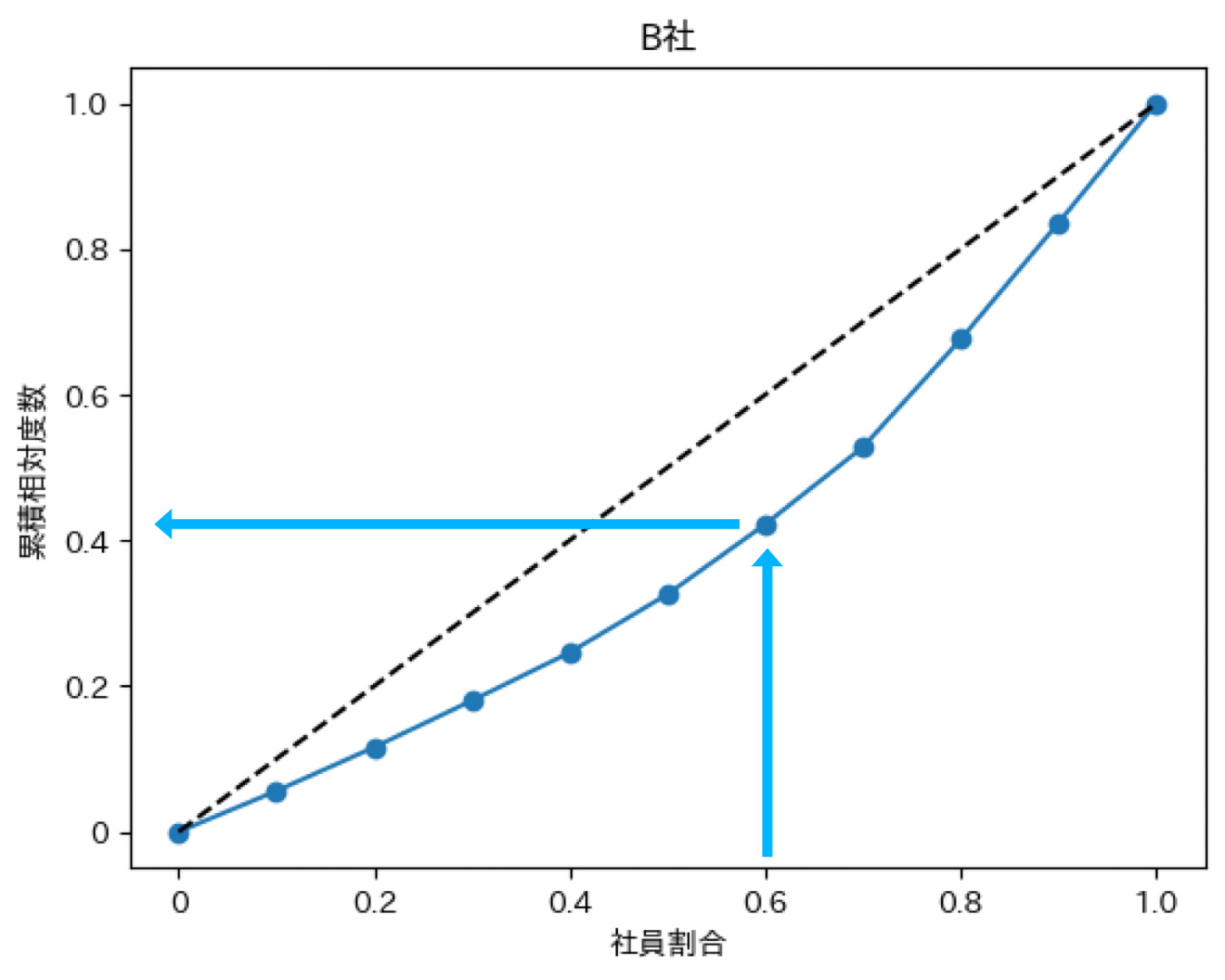
↑の図を見て欲しいのですがX軸が0.6、つまり全体の6割なので今回の場合は社員6人です。
それに対して累積相対度数(各々がもらっている給料を累積したもの)が0.422となっています。
これが表す意味としては、社員全体の60％で給料の総額の42.2%しかもらっていないという事です。

そのため、偏りがあればあるほど完全平等線とローレンツ曲線の距離が離れていくのです。

 

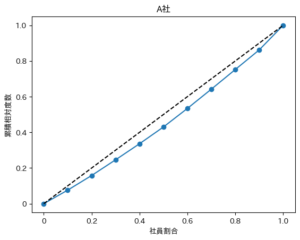
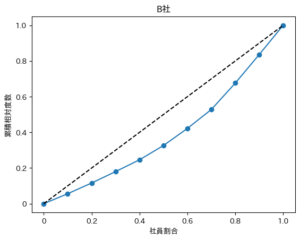
もう一度A社とB社の結果を見比べてみましょう！
明らかにB社の方がスペースが大きいため、視覚的にも偏りが大きい事がわかりますね！

 

 

ジニ係数とは？

ジニ係数は、0から1までの値をとり、0に近いほど所得格差が小さく、1に近いほど所得格差が大きいことを示す指標です。
ローレンツ曲線をもとに、1912年にイタリアの統計学者、コッラド・ジニによって考案されました。

 

ジニ係数の求め方

ジニ係数は、ローレンツ曲線と完全平等線との間の面積を2倍して算出されます。
以下の図の黄色い面積の2倍の値がジニ係数です。

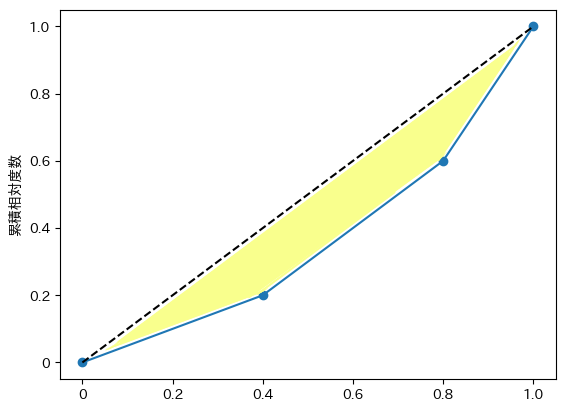
では早速上記のジニ係数を求めてみましょう。
このジニ係数の累積相対度数は↓です。

X軸(横軸)	Y軸(縦軸)
0.4	0.2
0.8	0.6
1	1

 

 

まずは↓の青い画像の三角形の面積を求めます。

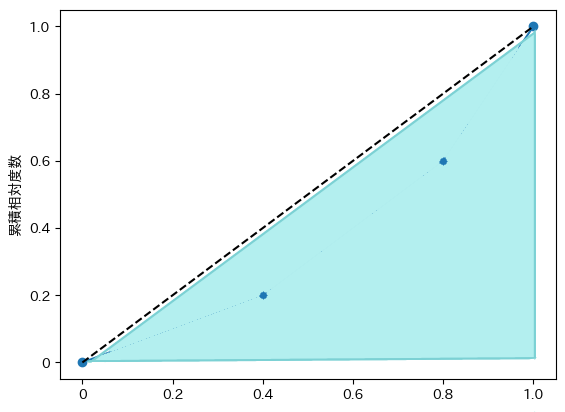
といっても、縦も横も1なので非常に簡単ですね。
「底辺×高さ÷2」で求められます。

$\frac{1×1}{2}=0.5$

 

簡単ですね。
月に↓の図のA,B,Cの面積を求めます。
一気に求める事は出来ないので、それぞれ分割して求めます。

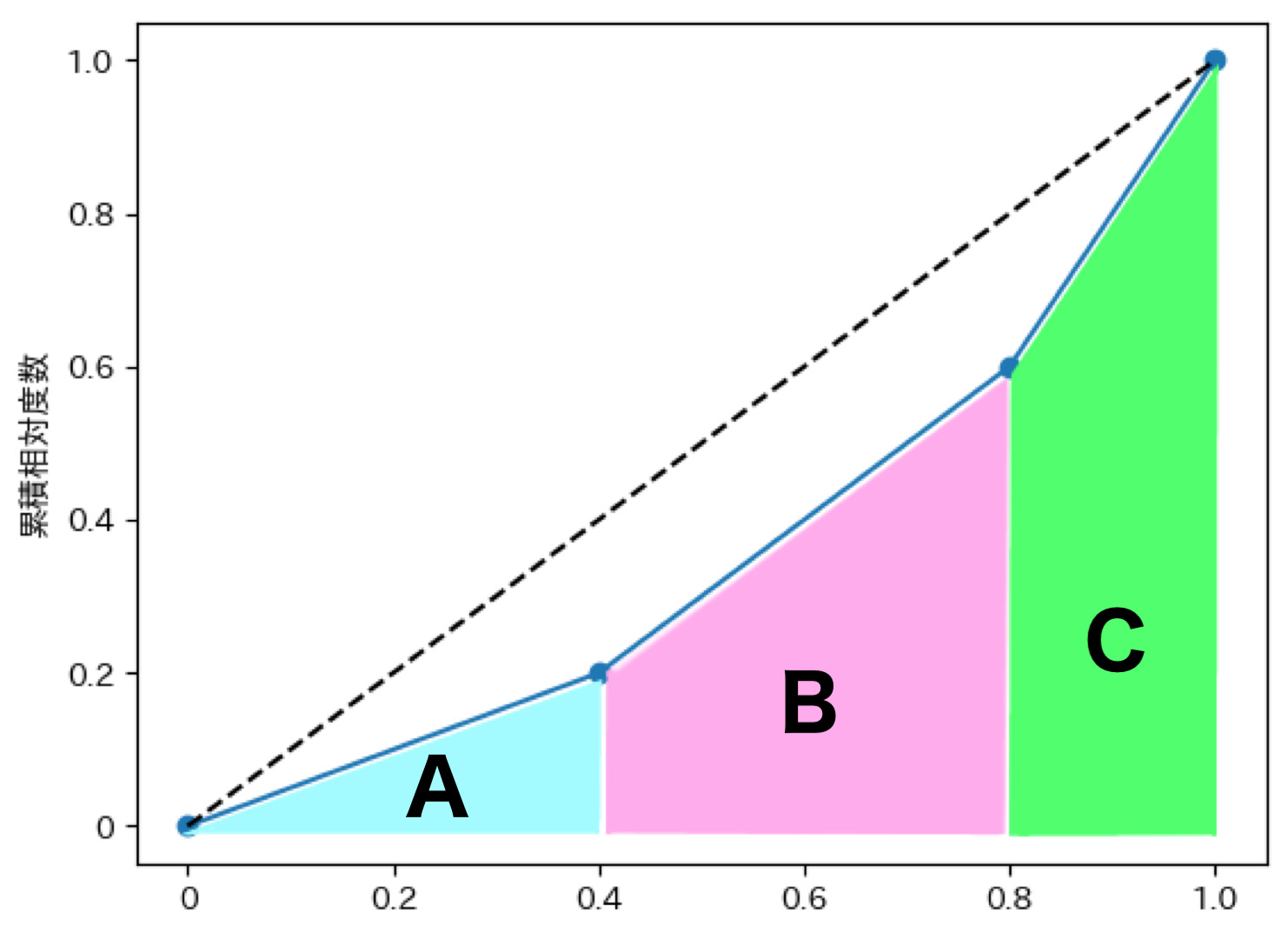
まずはAの面積を求めます。

累積相対度数表から、Aは横が0.4で縦が0.2という事が分かっています。
ですので、先ほどと同じように面積を求める事ができますね！

$\frac{0.4×0.2}{2}=0.04$

 

Aの面積が0.04という事が分かりました。
次にBの面積を求めます。

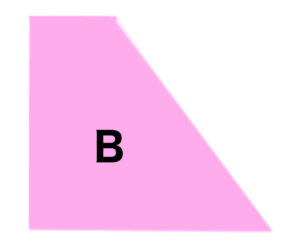
そのままだと分かり辛いので、Bを90度回転させました。
そうすると、Bは台形という事に気付きますね！

台形の公式は↓でしたね？覚えていますか？

この時上底は、X軸で0.4の時のY軸の値。
下底はX軸で0.8の時のY軸の値ですので↓になります。

• 上底：0.2
• 下底：0.6

高さは$0.8-0.4=0.4$です。
これらの数字を基に台形の面積を求めてみましょう。

$\frac{(0.2+0.6)×0.4}{2}=0.16$

 

Bの面積が0.16という事が分かりました。
最後にCの面積を求めましょう。

• 上底：0.6
• 下底：1

ですので、高さは$1-0.8=0.2$ですね！

$\frac{(0.6+1)×0.2}{2}=0.16$

 

Cの面積も分かりました。
まとめると、↓になります。

 

そして最後にA、B、Cの面積を足して2をかければジニ係数を求められます。

$(0.04+0.16+0.16)×2=0.28$

結果、ジニ係数は0.28という事が分かりました。
この様にしてジニ係数をもとめる事ができます。

 

 

 

確率の基本情報【0から始める統計検定2級講座⑦】この講座の対象者は以下の方を想定しています。 数学は中学レベルしか分からないけど統計検定2級に合格したい どの参考書...

Work illustrations by Storyset