この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 正規分布ってなに?
- 標準正規分布はどう使うの?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回は、統計学の中でも非常に重要な正規分布について解説します。
正規分布は統計の理解を深める上で、基礎となる部分ですのでしっかりと押さえておきましょう。
正規分布とは何か?
正規分布は統計において最も重要な連続型確率分布です。
実は普段生活している中でも、正規分布の例に触れている事は非常に多いのです。
今回の講座では、名前からも品格が漂う正規分布について解説します。
まず正規分布がどんなものかと言うと、↓の図のような確率分布です。
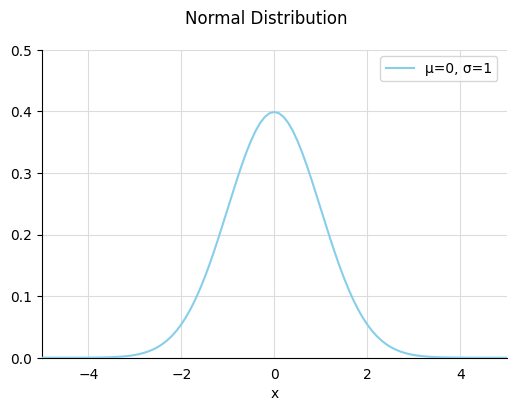
これが何を意味しているかというと、例えば日本全体の男性の平均身長を考えてください。
この平均身長が170cmだとしたら、全員が170cmというわけではありませんよね?
人によっては、180cmであったり、169cmだったりします。
しかし、確率としては180cmよりも平均値に近い169cmの方が高くなるのは感覚からもわかると思います。
あなたの周りの男性も、170cmに近い人のほうが多く、180cm以上であったり160cm以下という人は少ないと思います。
正にイメージ的には上記の図の横軸(x軸)が0周辺の方が確率が高く、離れるほど下がっていく事が視覚的にも分かりますね。
ちなみに正規分布の例としては他にも↓の物があります。
- 学力テストの点数の分布
- 工場が製品を作った時の重量のバラつき
- ニワトリが生む卵の大きさの分布
もちろんこれだけには収まらず、無数にあります。
なぜ正規分布になるのか?
でもなぜ正規分布に従うのか?理由が気になりますよね?
しかし、じつはその理由はわかっていません。
そのメカニズムは解明されておらず、様々な観測の結果から発見されたのです。
正規分布の確率密度関数
正規分布の確率密度関数は↓の式で表されます。
\begin{equation}
f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}
\end{equation}
非常に複雑ですね。
記号の意味としては下記の通りです。
- $\sigma$:標準偏差
- $\sigma^2$:分散
- $e$:ネイピア数
この様になっています。
正規分布の平均と分散
統計学の言い回しとして、確率変数$X$が上記のような確率密度関数を持つとき、$X$は「平均$μ$、分散$\sigma^2$の正規分布に従う」という言い方をします。
また、平均$μ$、分散$\sigma^2$の正規分布を、↓のように表します。
$N(μ, \sigma^2)$
確率変数$X$が$N(μ, \sigma^2)$に従う時、正規分布の平均は↓になります。
$E(X)=μ$
また、正規分布の分散は↓になります。
$V(X)=\sigma^2$
様々な正規分布のグラフの形
ここでもう一度先ほど見た図を見てみましょう。
やまの頂点に対応する$X$が平均$μ$になります。この場合は0ですね。
平均から離れるにつれ、確率密度(Y軸)は低くなっています。

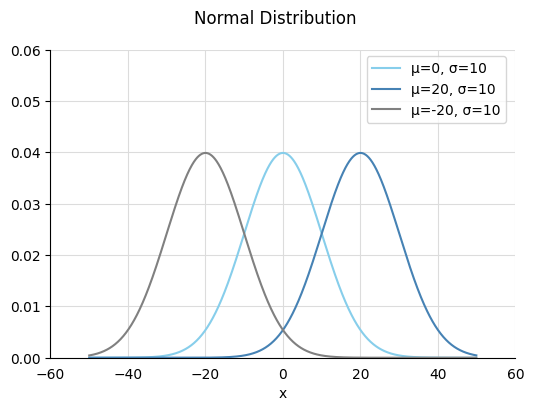
平均値が[-20, 0, 20]で分散が一緒の場合は↓のように横にそのまま移動します。
値が高くなればなるほど右にスライドしていっていますね。
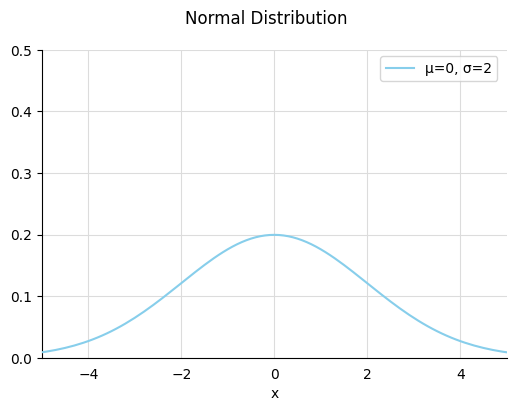
続いて、標準偏差が変化した場合です。
平均は2つとも0で、標準偏差が$\sigma=1$の場合と$\sigma=2$の場合で↓の様に変わります。
標準偏差はバラつきを表すものでしたので、値が高いほど平均値を取る確率が下がり、山がなだらかになっています。
正規分布の再生性
また正規分布には再生性があります。
これは、簡単に言うと↓の通りです。
$N(μ_1, \sigma_1^2)+N(μ_2, \sigma_2^2)=N(μ_1+μ_2, \sigma_1^2+ \sigma_2^2)$
要は、2つの独立した正規分布に従うデータがあるとき、それを足し合わせた平均と分散は、単純に足した値になるという事です。
例えば以下の2つの平均と分散があります。
- $μ_1:50$ $\sigma_1^2:6$
- $μ_2:65$ $\sigma_2^2:9$
これらを足した場合の平均と分散は↓になります。
$N(115, 15)$
標準正規分布とは?
統計学において、非常に重要な分布として標準正規分布という物があります。
標準正規分布は平均0、分散1の正規分布の事です。$N(0, 1^2)$
図で表すと↓のように、0を頂点とし分散が1です。
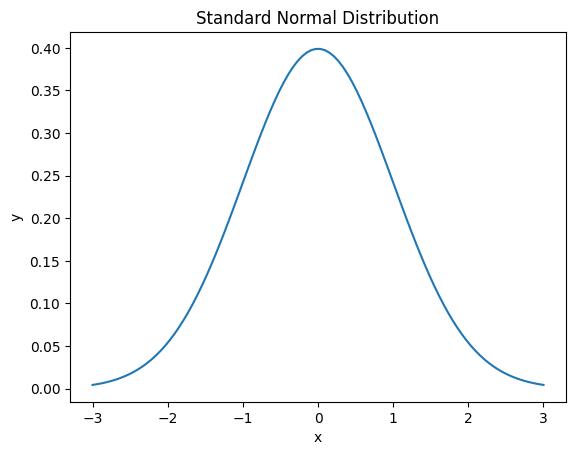
標準化
確率変数$X$が平均$μ$、分散$\sigma^2$の正規分布に従う時、$X$から平均$μ$を引いて、標準偏差$\sigma$で割った値を標準化得点$z$とします。
すると$z$は平均が0、分散が1の標準正規分布に従うのです。
式で表すと↓になります。
$z=\frac{X-μ}{\sigma}$
この疑問の結論をいきなり言ってしまうと、データ同士を比べやすくするためです。
データによっては単位が全然違ったり、平均値が全く違うなど往々にしてあります。
そのため尺度を揃えて比べ安くするのが標準化です。
じつは前の講座でもこの点の解説をしていますので、忘れてしまった方は↓の講座をどうぞ!

まとめ
今回の内容をまとめますと、
- 正規分布は、確率論や統計学で用いられる連続的な変数に関する確率分布の一つ。
- データが平均値の付近に集積するような分布を表す。
- 主な特徴としては、平均値と最頻値、中央値が一致する事や、平均値を中心にして左右対称である。
- 平均0、分散1の正規分布を標準正規分布という。
となっています。
正規分布を初めて聞いたという人には「ふ~ん、そんなのがあるんだ。」位かもしれませんが、これが非常に重要なものなのです。
次回以降にさらに深堀りしていきます。
Work illustrations by Storyset