この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 指数分布ってなに?
- 離散型と連続方の一様分布って違うの?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回は指数分布と一様分布について詳しく解説していきます。
指数分布とは?
指数分布とは、確率論および統計学における連続確率分布の一種で、ある事が起こってから、次に起こるまでの期間のように、次に何かが起こるまでの期間が従う確率分布です。
例えば、事故が起きてから次に事故が起きるまでの期間や、地震が起きてから次に地震が起きるまでの期間などがそれに当たります。
ある期間に平均して$\lambda$(ラムダ)回起こる現象が、次に起こるまでの期間$X$が指数分布に従うとき、$X=x$となる確率密度関数は次に式で表されます。
$f(x) = \lambda e^{-\lambda x} , \quad x \ge 0$
$\lambda$は指数分布のパラメータです。
また、必ず正の値を取ります。
指数分布がよく使われるシーン
指数分布は次のようなシーンでよく使われます。
- ある事象が起こるまでの時間を記述する。
- ある事象が起こる回数を記述する。
- ある事象が起こる間隔を記述する。
指数分布の性質
指数分布の性質として主に以下の特徴があります。
- 平均値と分散は$\lambda$に等しい。
- 左端が急峻で、右端がゆるやかに減少する。
- 無記憶性である。
それぞれを深堀りしていきましょう。
指数分布の平均値と分散
指数分布の平均値と分散は以下の式で表されます。
- $E(X)=\frac{1}{\lambda}$
- $V(X)=\frac{1}{\lambda^2}$
左端が急峻で右端がゆるやかに減少する
これはグラフを見るのが一番ですね。
まず、下記の例を見てみましょう。
1時間に5個売れる商品がある。この商品が売れてから次の商品が売れるまでの時間が5分、10分、15分、20分、30分の場合のそれぞれの確率密度を求めよ。
まず、一時間に5個とあるので、$\lambda=5$です。
次に$x$に次の商品が売れるまでの時間を入れるのですが、時間と分の単位を揃えるために、以下の様にします。
- 5分=$\frac{1}{12}$
- 10分=$\frac{1}{6}$
- 15分=$\frac{1}{4}$
- 20分=$\frac{1}{3}$
- 30分=$\frac{1}{2}$
そしたら、$x$と$\lambda$が分かったので、先ほどの式に代入する事で、確率密度を求める事ができます。
$f(x) = \lambda e^{-\lambda x} $
$f(\frac{1}{12}) = 5 e^{-5×^\frac{1}{12}} =3.30$
この様にして、5分の場合の確率密度は$3.30$だと言う事が分かりました。
続いて、その他の時間も計算してまとめたのが下記の表です。
| 次に売れるまでの時間(分) | 次に売れるまでの時間 | 確率密度 |
| 5 | $\frac{1}{12}=0.083$ | 3.30 |
| 10 | $\frac{1}{6}=0.16$ | 2.17 |
| 15 | $\frac{1}{4}=0.25$ | 1.43 |
| 20 | $\frac{1}{3}=0.33$ | 0.94 |
| 30 | $\frac{1}{2}=0.5$ | 0.41 |
この表をグラフにすると以下の左端が急峻で、右端がゆるやかに減少する図になります。
縦軸(Y軸)は確率密度で、横軸(X軸)は$X$(次に売れるまでの時間)です。

離散一様分布とは?
一様分布には離散型と連続型があります。
まずは離散型から学んでいきましょう。
まず離散一様分布の説明です。
離散一様分布とは、確率論や統計学における離散確率分布の一種であり、有限集合の全ての値について、等しく確からしい場合である。
簡単に言うと、すべての事象の起こる確率が等しい離散型の分布の事です。
確率変数$X$が離散一様分布に従う時、$X=k$となる確率$P(X=k)$は、$N$を確率変数$X$の取りうる個数とすると次の様に計算できます。
$P(X=K)=\frac{1}{N} \quad (k=1,2,…,N)$
離散型一様分布の例
離散一様分布は、次のような場面によく使われます。
- サイコロの目の値を記述する。
- コインを投げたときの表の出る確率を記述する。
- ルーレットの数字が出る確率を記述する。
離散型一様分布の期待値と分散
期待値と分散は以下のようになります。
- $E(X)=\frac{N+1}{2}$
- $V(X)=\frac{N^2-1}{12}$
ではサイコロを例に、期待値と分散を求めてみましょう。
まず、それぞれの目(1~6)が出る確率ですが、離散型一様分布の場合は下記の式で求められるのでした。
$P(X=K)=\frac{1}{N}=\frac{1}{6}=0.166$
では続いて期待を公式に当てはめると以下の様になります。
$E(X)=\frac{6+1}{2}=3.5$
分散は次の式で求められます。
$V(X)=\frac{6^2-1}{12}=2.9$
連続一様分布とは?
連続一様分布とは、確率論や統計学における連続確率分布の一種であり、分布上の同じ長さの区間が等しく確からしい場合です。
台は2つの母数aとbで定義され、それぞれ最小値と最大値です。
確率密度関数は下記になります。
$f(x)=\frac{1}{b-a}$ $(a \leqq X \leqq b)$
例えば、最小値がaが2で、最大値bが5である場合をみてみましょう。
$2 \leqq X \leqq 5$をプロットすると↓になります。
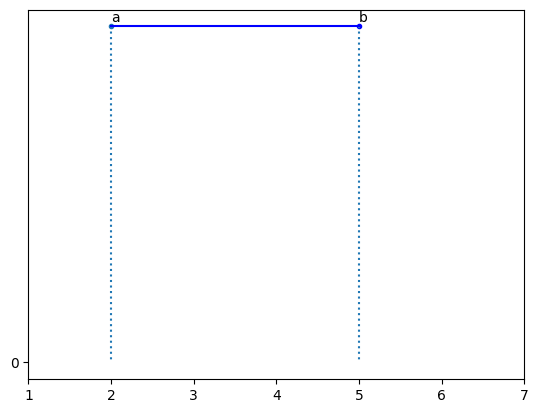
$2 \leqq X \leqq 5$の範囲の確率は、
$f(x) = \frac{1}{5-2}=\frac{1}{3}$となります。
連続一様分布の期待値と分散
連続一様分布の期待値と分散は以下の通りです。
- 期待値:$E(x)=\frac{a+b}{2}$
- 分散:$V(X)=frac{b-a}^2{12}$
例題
1日の勉強時間が15分から60分の人を対象にしたアンケート結果が一様分布に従う場合、勉強時間が45分以上である確率はいくらとなるか求めよ。
まず問題文から最小値と最大値は以下の様になります。
- 最小値:15分
- 最大値:60分
そして今回求めたいのは以下の図の青い分部の面積です。
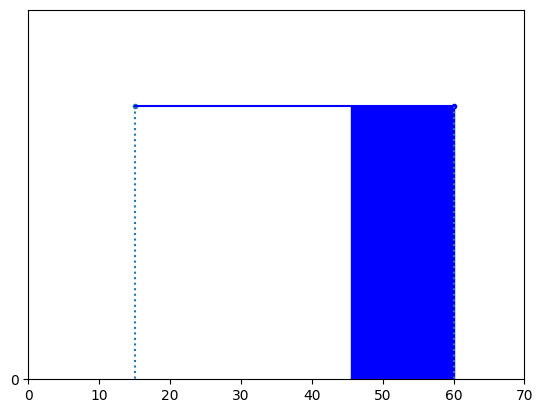
この面積は以下の様にして求める事ができます。
$P(45 \leqq X \leqq 60)=\frac{1}{60-15}×(60-45)=\frac{1}{3}$
この様にして、$frac{1}{3}$と求める事ができます。















