95%信頼区間とは？【0から始める統計検定2級講座⑲】

この講座の対象者は以下の方を想定しています。

この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。

今回は統計学における非常に重要な要素の信頼区間について解説します。

95%の確率なら「確実」と言えるのか？

「検定の結果、95%の確率で一致している。」
「この薬は98%の確率で効果が表れている。」

このように、確率的に非常に高い場合、何％なら確実と言って良いのか？
気になりますよね？

 

95%のデータが収まる範囲

以前にコチラの講座では、「平均±標準偏差×2」の範囲にデータ全体の95.4%が収まる」という話しをしました。

 

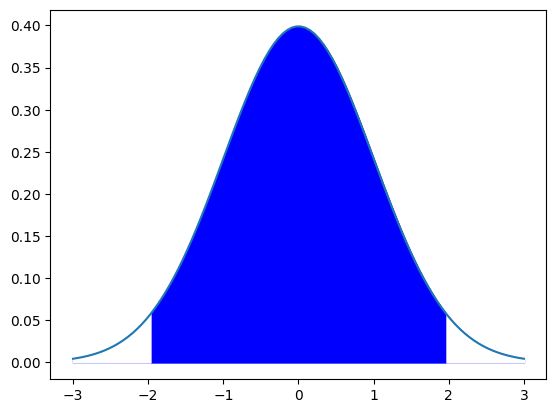
式で表すと$P(-1.96 \leqq Z \leqq 1.96)=0.95$です。
これは前に使った標準正規分布表から求める事ができます。

 

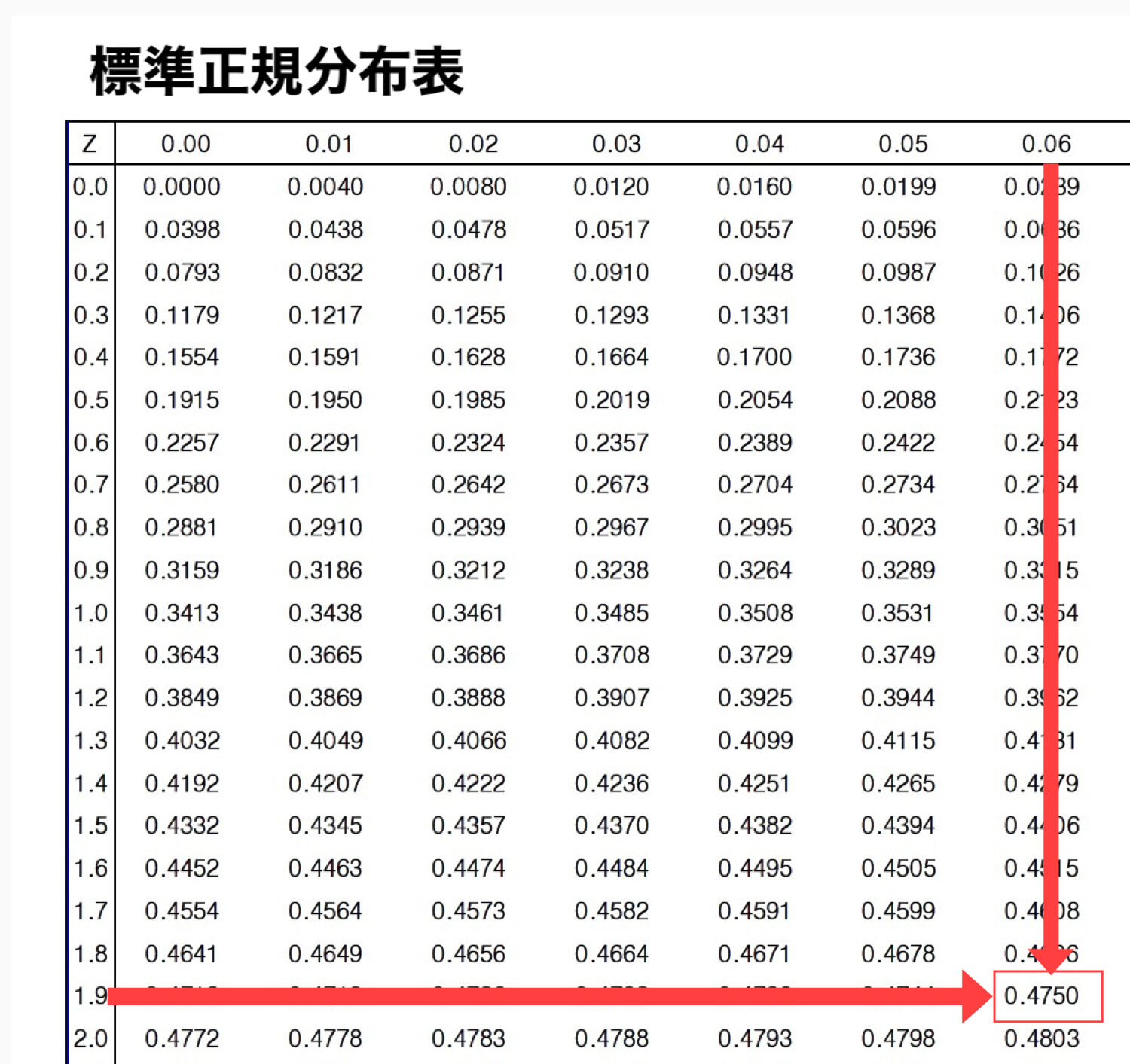
行が「1.9」、列が「0.06」に対応する値が「0.4750」です。
この場合、両側確率なので単純に倍にすると、

$0.4750×2=0.95$

となります。

 

95%の範囲を求める

上記の事をまとめると、正規分布$N(μ, \sigma^2)$に従う確率変数$X$は

の範囲に全体の95%が収まります。
$\sigma$が標準偏差で$μ$は平均です。

 

 

では実際に例題を基に、95%の範囲を求めてみましょう。

まず平均と分散を求めます。

6の目が出る回数は二項分布で求める事ができるのでした。
当たり前ですが、6の目が出る確率は$\frac{1}{6}$ですね。

二項分布$B(50, \frac{1}{6})$に従っているので、平均$E(X)$と分散$V(X)$は以下の様に求められます。

 

$E(X)=60×\frac{1}{6}=10$…平均

$V(X)=60×\frac{1}{6}×(1-\frac{1}{6})=\frac{50}{6}=\frac{25}{3}$…分散

 

n=60は十分に大きいとみなして良いので、正規分布に近似します。
6の目が出る回数を$X$とすると、以下の式に平均と標準偏差を代入する事で求められます。(上記で求めたのは分散ですので標準偏差にするのを忘れないように！)

 

$-1.96\sigma+μ \leqq X \leqq 1.96\sigma+μ$

$-1.96×\sqrt{\frac{25}{3}}+10 \leqq X \leqq 1.96×\sqrt{\frac{25}{3}}+10$

$4.341 \leqq X \leqq 15.658$

 

この様にして、「4.341回～15.658回」が95%の範囲だという事が分かりました。
ちなみに、整数で表す場合は、単純に四捨五入すれば良いわけではありません。

95%以上にする必要があるので、「4回～16回」とするのが答えです。

 

 

区間推定とは？

区間推定という単語を初めて聞いた人も多いと思います。
簡単に説明すると、区間推定は母集団の真の値が含まれることが、かなり確信できる数値範囲のことです。
前セクションでやったように、区間で推定するので区間推定です。

 

信頼区間

この区間の事を「信頼区間」と言い、

• 90%信頼区間
• 95%信頼区間
• 99%信頼区間

などどいった区間を求める事もありますが、統計検定では「95%信頼区間」が使われる事が多いです。

 

 

95%信頼区間の求め方

では実際に95%信頼区間を求めてみましょう。
以下の問題について考えます。

このように、ストップウォッチなどで計測する場合は真の値であるタイムと、計測結果にどうしてもズレが生じるものです。
今回の場合はそのズレが標準偏差0.4秒と分かっています。
ちなみに、

そして、このようなズレは正規分布に従う事が知られています。

ではどの様に求めるのか？ですが、問題文を整理すると下記の不等式が成り立ちます。
これを解いてみましょう。

 

$μ-1.96×0.4 \leqq 7.2 \leqq μ+1.96×0.4$

まずは3辺から$μ$を引きます。

$-1.96×0.4 \leqq 7.2 -μ \leqq 1.96×0.4$

次に、$7.2$を引いていきます。

$-1.96×0.4 -7.2 \leqq -μ \leqq 1.96×0.4 -7.2$

計算します。

$-7.984 \leqq -μ \leqq -6.416$

そして$-μ$から$-$をとるために3辺に$-1$を掛けます。
(不等号が逆になります。)

$7.984 \geqq μ \geqq 6.416$

$6.416 \leqq μ \leqq 7.984$…答え

この様にして、95%信頼区間は$6.416 \leqq μ \leqq 7.984$と推定する事ができました。

 

95%信頼区間の注意点

95%信頼区間の大事なポイントとして、「計測タイムから$μ$の信頼区間を求める事を繰り返すと、100回のうち95回は真の値を含んでいる信頼区間である」という事です。

真の値が$6.416 \leqq μ \leqq 7.984$になる確率が95%であるという事とは違いますので、注意が必要です。

 

 

練習問題

①

 

 

WorStorysetk illustrations by