この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 大数の法則ってなに?
- 中心極限定理の意味が分からない
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回は統計学における重要な法則である、大数の法則と中心極限定理について詳しく解説していきます。
大数の法則とは?
統計学では、大数の法則という非常に重要な法則があります。
理解は難しくないので、しっかりと押さえていきましょう。
前回の講座では、母集団から標本を抽出するのを何度も繰り返すと標本平均の平均は母平均に一致する事を学びました。
しかし、標本抽出を何度も繰り返さなくても標本平均$\bar{X}$を母平均$μ$に近づける方法があります。
それが大数の法則です。
大数の法則
大数の法則は非常にシンプルです。それは、
サンプルサイズ$n$を大きくしていくと、標本平均$\bar{X}$は母平均$μ$に一致する。
これが大数の法則です。
極端な例ですが、母集団100人に対して標本が10人などでは無く、50人、70人、90人と増やしていく事で、標本平均と母平均が一致するというものです。
実際にそうなるのかpythonを使って、以下の例を見てみましょう。
身長平均が170で標準偏差10の正規分布に従うデータをランダムに生成する。
サンプルサイズが10、100、10000の場合の標本平均を求めよ。
この検証をしてみたいと思います。
サンプルサイズ10の場合
|
1 2 3 4 5 6 |
import numpy as np # 平均170、標準偏差10の正規分布に従う10個のランダムデータを作成する data = np.random.normal(170, 10, 10) data.mean() |
->167.97303132944137
サンプルサイズ100の場合
|
1 2 3 4 |
# 平均170、標準偏差10の正規分布に従う100個のランダムデータを作成する data = np.random.normal(170, 10, 100) data.mean() |
->168.8766712631108
サンプルサイズ10000の場合
|
1 2 3 4 |
# 平均170、標準偏差10の正規分布に従う10000個のランダムデータを作成する data = np.random.normal(170, 10, 10000) data.mean() |
->170.02984011911815
この様な結果となりました。
やはりサンプルサイズが一番大きい10000の場合が、一番母平均の値に近い結果となりました。
上のコードは常にランダムな結果をもってくるので実行する度に違う結果が返ってきますが、基本的にはサンプルサイズが大きいほど母平均に近くなる確率が高いです。
中心極限定理
つづいて中心極限定理です。
これは、下記のような定理です。
標本平均$\bar{X}$は、標本の大きさ$n$がじゅうぶんに大きいと、平均$μ$、分散$\frac{\sigma^2}{n}$の正規分布に近似的にしたがう。
これは、サンプルサイズ(標本の大きさ)がじゅうぶんに大きい時は、母集団の分布がどんな形であれ、標本平均$\bar{X}$の分布は正規分布に近似するというものです。
ようは、母集団が一様分布であっても、標本平均$\bar{X}$の分布は正規分布に近似するのです。
正規分布のおさらい
正規分布を忘れてしまったという方のために簡単におさらいします。
正規分布は、データが平均値を中心に左右対称に分布する確率分布です。正規分布は、身長、体重、IQなど、多くの現象に適用できます。正規分布の性質は、次のとおりです。
- 平均値と最頻値が一致する
- 左右対称である
- 平均値を中心にして、左右に一定の割合でデータが分布する
- 平均値から離れるほど、データが分布する割合は減少する
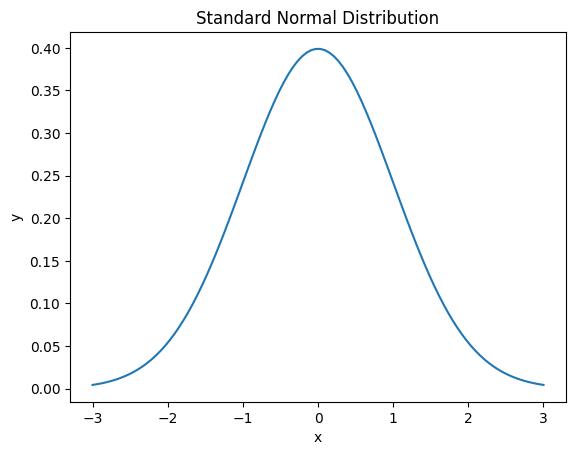
詳しくはコチラを参照してください。
サイコロの例
では中心極限定理をサイコロを例にとって考えてみましょう。
サイコロは1~6の目が出る確率は全て等しいので、一様分布になります。
母平均$μ$と母分散$\sigma^2$は以下の様になります。
- $μ=3.5$
- $\sigma^2=2.92$
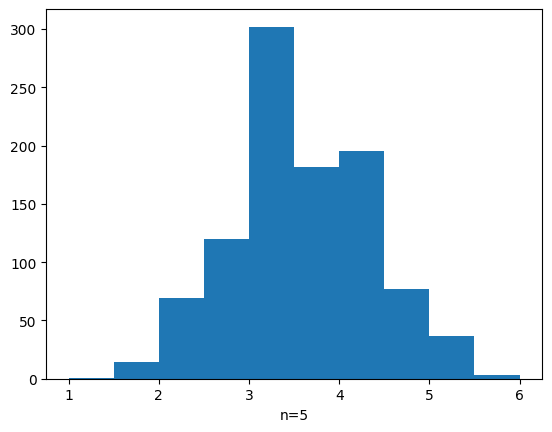
例えば、サイコロを5個(n=5)振って、出た目の平均を求める検証を1000回行った時の結果は以下になります。
基本的には平均周辺の確率が高く、平均から離れるほど確率が下がっているのが分かりますが、いびつな形をしています。
続いて、サイコロを100個(n=100)の場合の結果はコチラです。
n=100にすると、平均を最頂にして、左右対象の確率分布になっていますね。
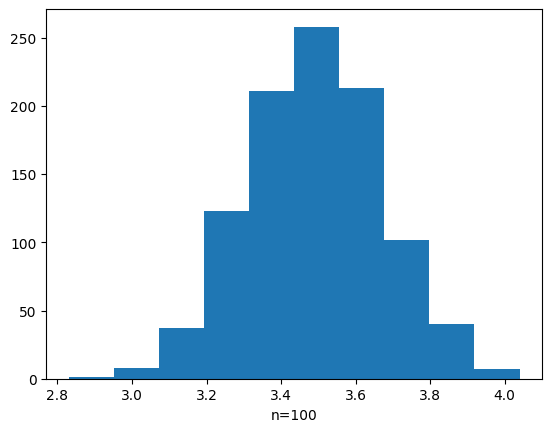
このように、サンプルサイズが100である後者の方が、ヒストグラムの形が正規分布に近似している事が分かります。














