この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 母平均の推定ってどうやるの?
- 母分散が分からない場合はどうやって推定するの?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回は母平均の推定についてです。
今回の講座から、標本から得られたデータを基に母集団の推定を行う推測統計学に入っていきます。
統計学が面白くなってくる部分ですので、楽しみながら学びましょう!
母平均の区間推定とは?
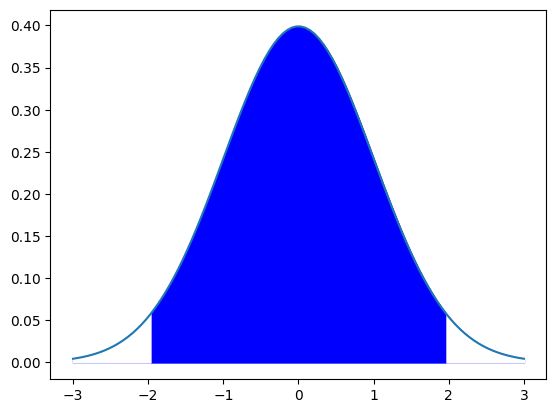
まず母平均の推定というのはどういうものか説明します。
ある学校から無作為に生徒100人を選んで学力テストを行った。
そのテストの結果、平均点は72点であった。
この結果を基に、この学校全体の平均点を95%信頼区間で推定せよ。
このように、母集団から採取した標本の結果を基に、母集団の平均を推定する事です。
言葉の意味そのままですね。
母平均の推定を行う際、まずどのような条件で推定を行うのかを知る必要があります。
具体的には以下の3つのパターンがあります。
- 母分散が分かっている場合の母平均の推定
- 母分散が分からないけど標本が大きい場合の母平均の推定
- 母分散が分からず、標本も小さい場合の母平均の推定(今回はやりません)
今回の講座では①と②の推定だけやります。
③は別の知識が必要になるので、今後の講座でやります。
他の推定
ちなみに母平均の推定以外にも、
- 母比率の推定
- 母平均が分かっている場合の母分散の推定
- 母平均が分からない場合の母分散の推定
などの推定を今後の講座で行いますので、楽しみにしておいてください。
区間推定とは?
上記の問題分の最後に、「95%信頼区間で推定せよ。」とあります。
これは、「母平均は75である」といった点で推定するのでは無く、母平均は「$68 \leqq X \leqq 78$の間である」といったように、区間で推定する事です。
またこの時、95%信頼区間とある意味は、母平均の95%信頼区間を求めるという作業を100回やったとして、95回はその区間の中に母平均が含まれるという意味です。
母分散既知の母平均の区間推定のやり方
では実際に母分散が分かっている場合の区間推定のやり方をみていきましょう。
主な流れとしては、母分散が分かっているので、標本平均を求めてから下記の式に代入する事で求める事ができます。
$\bar{X}-1.96×\frac{\sigma}{\sqrt{n}} \leqq μ \leqq \bar{X}+1.96×\frac{\sigma}{\sqrt{n}} $
なぜこの様な式になるのかはコチラの講座でやりましたね。
この講座で使った式は↓でした。
$-1.96\sigma+μ \leqq X \leqq 1.96\sigma+μ$
しかし、今回は標本平均$\bar{X}$の分布ですので、$μ$を$\bar{X}$に置き換え、また$\sigma$は$\frac{\sigma}{\sqrt{n}}$にしています。
例題
下記の例題をもとに解説します。
ある学校の男子生徒100人の身長を測定したところ、標本平均は171cmであった。この学校の全男子生徒の平均身長の95%信頼区間を求めよ。
母分散は$\sigma^2=7^2$である。
この問題文から分かる事として、
- 標本の大きさ$n=100$
- 標本平均$\bar{X}=171$
- 母分散$\sigma^2=7^2$→標準偏差$\sigma=7$
という事が分かっています。
標本平均も既に分かっていますね。
これを先ほどの式に代入すると、95%信頼区間を求める事ができます。
$\bar{X}-1.96×\frac{\sigma}{\sqrt{n}} \leqq μ \leqq \bar{X}+1.96×\frac{\sigma}{\sqrt{n}} $
$171-1.96×\frac{7}{\sqrt{100}} \leqq μ \leqq 171+1.96×\frac{7}{\sqrt{100}} $
$171-1.96×\frac{7}{10} \leqq μ \leqq 171+1.96×\frac{7}{10} $
$171-1.372 \leqq μ \leqq 171+1.372$
$169.628 \leqq μ \leqq 172.372$…答え
この様にして、95%信頼区間が169.628~172.372だと言う事が分かりました。
これが母分散が分かっている場合の母平均の推定です。
しかし、現実的には母平均が分からないのに母分散が分かっているという状況はほとんどありません。
母分散が分からな状況で、母平均の推定を行う事がほとんどです。
母分散が分からない場合の母平均の推定
続いて、母分散が分からない場合の母平均の推定のやり方を見ていきましょう。
ちなみに今回は標本が大きいという条件付です。
標本が大きいというのは大体$n=30$以上の標本を指します。
これ以下の場合は、t分布の知識が必要になるので、今後の講座で紹介します
母分散が分からない場合の対処方
では母分散が分からない場合にはどのようにして母平均の推定をすれば良いのでしょうか?
これには次の2つの定理が非常に重要になってきます。
標本平均$\bar{X}$は、標本の大きさ$n$がじゅうぶんに大きいと、平均$μ$、分散$\frac{\sigma}{\sqrt{n}}$の正規分布に近似的にしたがう。
これは中心極限定理という物でしたね。
もう一つの定理として、標本分散の一致性があります。
標本のおおき$n$がじゅうぶんに大きいと、標本分散$S^2$、不偏分散$U^2$はどちらも母分散$\sigma^2$に一致する。
これも前回の講座でやったやつですね。
この定理を取り入れて、先ほどの母分散既知の場合の母平均の推定の公式を変形させると、
$\bar{X}-1.96×\frac{\sigma}{\sqrt{n}} \leqq μ \leqq \bar{X}+1.96×\frac{\sigma}{\sqrt{n}} $
↓
$\bar{X}-1.96×\frac{S}{\sqrt{n}} \leqq μ \leqq \bar{X}+1.96×\frac{S}{\sqrt{n}} $
この様になります。
そう、母分散(母標準偏差)ではなく標本分散(標本標準偏差)を使えば良いだけなのです。
非常に簡単ですね。
例題
では実際に例題を解いてみましょう。
あるパン屋でメロンパンを販売している。このメロンパン81個の重さを調べたところ、平均120gで標準偏差が5であった。
1個あたりの重さの母平均を、95%信頼区間で推定せよ。
問題文を整理すると、
- $n=81$
- $\bar{X}=120$
- $S=5$
という事が分かります。
$n$も$80$あるために大標本という事が言えます。
これを先ほどの式に代入していきます。
$\bar{X}-1.96×\frac{S}{\sqrt{n}} \leqq μ \leqq \bar{X}+1.96×\frac{S}{\sqrt{n}} $
$120-1.96×\frac{5}{\sqrt{81}} \leqq μ \leqq 120+1.96×\frac{5}{\sqrt{81}} $
$120-1.96×\frac{5}{9} \leqq μ \leqq 120+1.96×\frac{5}{9} $
$120-1.96×\frac{5}{9} \leqq μ \leqq 120+1.96×\frac{5}{9} $
$118.911,,, \leqq μ \leqq 121.088,,,$…答え
この様にして求める事ができます。
まとめ
母分散が分からず、大標本の場合に母平均の95%信頼区間を求めるには下記の式に代入するだけですので、非常に簡単です。
こういった問題も統計検定2級では頻出ですので、しっかりと覚えておきましょう。
$\bar{X}-1.96×\frac{S}{\sqrt{n}} \leqq μ \leqq \bar{X}+1.96×\frac{S}{\sqrt{n}} $
練習問題
①
答え:$171.648 \leqq μ \leqq 176.352$
母分散が分かっているので、下記の式を解く事で求める事ができます。
$174-1.96×\frac{12}{\sqrt{100}} \leqq μ \leqq 174+1.96×\frac{12}{\sqrt{100}} $
$171.648 \leqq μ \leqq 176.352$
②
答え:$79.55 \leqq μ \leqq 84.45$
母分散は分からないですが、$n=144$ですので、大標本と言えます。
下記の式から解く事ができます。
$82-1.96×\frac{15}{\sqrt{144}} \leqq μ \leqq 82+1.96×\frac{15}{\sqrt{144}} $
$79.55 \leqq μ \leqq 84.45$














