t分布で母平均を推定しよう！【0から始める統計検定2級講座㉗】

この講座の対象者は以下の方を想定しています。

この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。

前に母分散が分かっている場合と、母分散が分からないけど大標本の場合の母平均の推定をやりましたね。

今回は、母分散が分からない状態かつ、標本が少ない時に母平均を推定する方法を教えます。

これをやるために、まずはt分布の理解が必要です。

 

t分布とは？

t分布は、統計学において母平均の推定、母数の分散の差の検定に用いられます。
また、信頼区間の推定や検定にも用いられます。

 

標準正規分布とt分布

前に、母集団が正規分布$N(μ, \sigma^2)$に従うとき、標本平均$\bar{X}$は平均$μ$、分散$\frac{\sigma}{n}$の正規分布にしたがうことはやりましたね。

そして、$\bar{X}$を標準化した事で求められる統計量$Z$は、

$Z=\frac{\bar{X}-μ}{\sqrt{\frac{\sigma^2}{n}}}$

標準正規分布$N(0, 1^2)$にしたがいます。

これに対して、t分布の場合は母分散が分からないので$\sigma^2$が使えません。
こんな時は不偏分散$U^2$を使うのでしたね！

 

不偏分散$U^2$を使った統計量$T$を求めるには以下の式から求める事ができます。

$Z=\frac{\bar{X}-μ}{\sqrt{\frac{U^2}{n}}}$

 

$Z$の式と$T$の式を見るとほぼほぼ一緒ですね。
母分散が$\sigma^2$が不偏分散$U^2$になっている位です。

そのため、統計量$T$は標準正規分布には従いません。
t分布に従うのです！

 

t分布のもつ特徴

t分布には以下のような特徴があります。

 

 

t分布の95％区間のの求め方

標準正規分布やカイ2乗分布と同じように、t分布も95%信頼区間を求める事ができます。

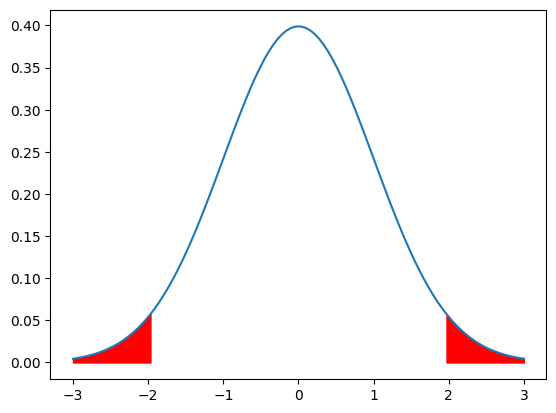
t分布は左右対象なので、↑の白い部分の面積が0.95になるようなパーセント点を求めれば良いのです。
また、t分布は自由度によって形が変わるので、その点も注意しながら下記のt分布表から対応する値を探せば良いのです。

 

t分布表

	0.005	0.01	0.025	0.05
1	63.657	31.821	12.706	6.314
2	9.925	6.965	4.303	2.920
3	5.841	4.541	3.182	2.353
4	4.604	3.747	2.776	2.132
5	4.032	3.365	2.571	2.015
6	3.707	3.143	2.447	1.943
7	3.499	2.998	2.365	1.895
8	3.355	2.896	2.306	1.860
9	3.250	2.821	2.262	1.833
10	3.169	2.764	2.228	1.812

左端の行の数値が自由度です。

例えば、自由度3の95%区間の%点を求めるには、両側検定なので「0.025」と自由度3のクロスする値「3.182」がパーセント点になります。

 

ですので、自由度3のt分布にしたがう確率変数$T$は、以下の範囲に全体の95%が収まります。

$-3.182 \leqq T \leqq 3.182$

 

 

 

母平均の推定：母分散が分からないかつ標本が少ない

ではt分布が分かった所で、母分散が分からない、かつ標本が少ない場合の母平均の推定手法を見ていきましょう。
主な流れとしては以下の通りです。

では実際に例題を見ながら解いていきましょう。

 

例題

標本が5と少ないですね～大体30よりも少ない場合はt検定で求めます。

 

標本平均$\bar{X}$と不偏分散$U^2$を求める

以下の式からまずは標本平均$\bar{X}$を求めます。

$\bar{X}=\frac{78+65+59+73+70}{5}=69$

 

続いて不偏分散$U^2$です。

$U^2=\frac{(78-69)^2+(65-69)^2+(59-69)^2+(73-69)^2+(70-69)^2}{5-1}=53.5$

 

これで、標本平均と不偏分散を求める事が出来ましたね！

• $\bar{X}=69$
• $U^2=53.5$

 

統計量$T$を求める

続いて下記の式から統計量$T$を求めます。

$T=\frac{\bar{X}-μ}{\sqrt{\frac{U^2}{n}}}$

->$T=\frac{69-μ}{\sqrt{\frac{53.5}{5}}}=\frac{69-μ}{\sqrt{10.7}}$

 

 

自由度$k-1$の%点($t$)を求める

今回は自由度$5-1=4$のt分布に従うので、t分布表から上側2.5%点に対応する値を求めます。

	0.005	0.01	0.025	0.05
1	63.657	31.821	12.706	6.314
2	9.925	6.965	4.303	2.920
3	5.841	4.541	3.182	2.353
4	4.604	3.747	2.776	2.132

「2.776」という事が分かりましたね。

 

これらの情報から統計量$T$は95%の確率で以下の範囲に収まります。

$-2.776 \leqq T \leqq 2.776$

ですので、統計量$T$に先ほどの値を代入し、不等式を解きます。

 

$-2.776 \leqq \frac{69-μ}{\sqrt{10.7}} \leqq 2.776$

まずは3辺に$\sqrt{10.7}$を掛けます。

-> $-2.776\sqrt{10.7} \leqq 69-μ \leqq 2.776\sqrt{10.7}$

次に3辺に-69します。

-> $-69-2.776\sqrt{10.7} \leqq -μ \leqq -69+2.776\sqrt{10.7}$

そして$-μ$を$μ$にするため3辺に-1を掛けます。

-> $69+2.776\sqrt{10.7} \geqq μ \geqq 69-2.776\sqrt{10.7}$

それぞれを計算します。

-> $78.08 \geqq μ \geqq 59.92$

不等式を整理して完成です。

-> $59.92 \leqq μ \leqq 78.08$…答え

 

 

練習問題

①

 

WorStorysetk illustrations by