この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 母分散の仮説検定はどうやるの?
- 母平均が分かっている場合と分からない場合でやり方は違う?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
前回は母平均がの仮説検定をやりましたので、続いて母分散の仮説検定です。
これも母平均が分かっている場合と分からない場合で求め方が変わりますので、その点もしっかりと押さえていきましょう!
母分散の仮説検定(母平均が分かっている場合)
まずは、母平均が分かっている場合のやり方を見ていきましょう。
以下のように、検定の流れは母平均の検定の流れと一緒です。
- 帰無仮説と対立仮説を立てる
- 検定統計量を求める
- 棄却域を設定
- 帰無仮説が正しいか検証
例題
ではさっそく例題を見ながら解き方を見ていきましょう。
ある塾の生徒全員が受けたテストの母平均が82点であった。
Aさんが友達5人に聞いたテストの結果が以下の通りであった。
[76点, 88点, 82点, 76点, 80点]
この結果から、母分散が25であるかどうかを、有意水準5%で検定しなさい。
帰無仮説と対立仮説
まず、問題文から母分散が25であるかどうかを検定したいので、両側検定になる事が分かります。
ですので、帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:$\sigma^2=25$
- 対立仮説:$\sigma^2 \neq 25$
検定統計量を求める
検定統計量$V$を求めるには以下の式から求める事ができます。
$V=\frac{(X_1-μ)^2+(X_2-μ)^2+…(X_n-μ)^2}{\sigma^2}$
今回は$n=5$のテスト結果は分かっているので、$X_1$から$X_5$までの値は分かっています。
また、母平均$μ$と分散$\sigma^2$は問題文から以下の通りです。
- $μ=82$
- $\sigma^2=25$
この値を、↑の式に当てはめてみましょう。
$V=\frac{(76-82)^2+(88-82)^2+(82-82)^2+(76-82)^2+(80-82)^2}{25}$
$V=\frac{36+36+0+36+4}{25}=4.48$…統計量$V$
このようにして、統計量$V=4.48$という事が分かりました。
棄却域の設定
母分散の検定を行う場合には何分布に従うのかと言うと、カイ2乗分布です。
カイ2乗分布は下記のように、自由度によって大きく形が変わる分布でした。
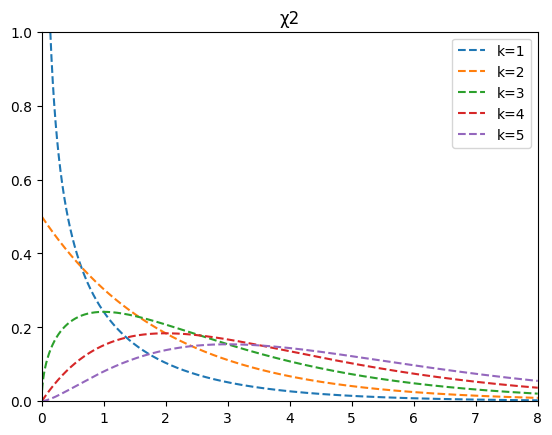
今回は自由度$k=5$で、有意水準5%の両側検定です。
ですので、カイ2乗分布表の自由度5で「0.025」と「0.975」に対する値が%点になります。
カイ2乗分布表を見ると、
| k | 0.025 | 0.05 | 0.95 | 0.975 |
| 5 | 0.83 | 1.15 | 11.07 | 12.83 |
境界値が「0.83」「12.83」だと言う事がわかります。
帰無仮説が正しいか検証
結果をまとめると、
- 検定統計量$V=4.48$
- 境界値:「$0.83$」「$12.83$」
という事が分かりました。
今回の検定統計量は、棄却域に含まれていませんね!
$0.83 < V(4.48) <12.83$
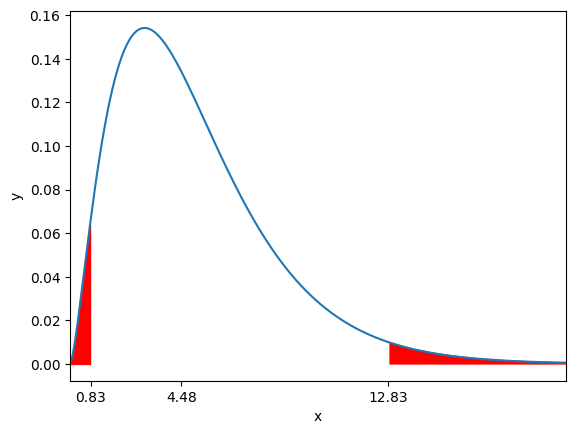
帰無仮説が棄却されず、対立仮説は採択されませんでした。
ですので、母分散は25と等しくないとはいえないという結論になりました。
母分散の仮説検定(母平均が分からない場合)
では続いて母平均が分からない場合の仮説検定のやり方を見ていきましょう。
母平均が分かっている場合との違い
ぶっちゃけ、そこまで大きな違いはありません。
下記の点にだけ注意してください。
- 母平均$μ$の代わりに標本平均$\bar{X}$を使う
- 自由度$k-1$のカイ2乗分布にしたがう
この2点だけです。
母平均が分からない場合は、前セクションでやった方法からこの2点が変わります。
例題
では、さっそく例題を基に解き方を見ていきましょう。
ある農家からメロンを仕入れている。
仕入れたメロンの重量を5個測ったところ、以下の値になった。
[1200g, 1150g, 1020g, 1290g, 1140g]
重量の標準偏差は50gと聞いていたが、本当はもっと大きいのではないかと疑惑がわいた。
本当に50gかどうか?有意水準5%で検定しなさい。
帰無仮説と対立仮説
問題文から標準偏差が50g以上かどうかを検定するので、上側検定を行います。
ですので、帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:$\sigma=50$
- 対立仮説:$\sigma > 50$
検定統計量を求める
母平均が分からない場合は、$\bar{X}$を使います。
検定統計量$V$を求めるには以下の式から求める事ができます。
$V=\frac{(X_1-\bar{X})^2+(X_2-\bar{X})^2+…(X_n-\bar{X})^2}{\sigma^2}$
まず、標本平均$\bar{X}$を求めます。
$\bar{X}=\frac{(1200+1150+1020g+1290g+1140)}{5}=1160$
対応する値を整理すると、
- $\bar{X}=1160$
- $\sigma^2=2500$
となります。
注意点として、問題文では$標準偏差\sigma=50$となっていましたが、必要なのは分散$\sigma^2$ですので、2乗しています。
これを上記の式に当てはめて統計量を求めます。
$V=\frac{(1200-1160)^2+(1150-1160)^2+(1020-1160)^2+(1290-1160)^2+(1140-1160)^2}{2500}$
$V=\frac{1600+100+19600+16900+400}{2500}=15.44$
検定統計量が$15.44$だという事が分かりました。
棄却域の設定
母分散の検定を行う際は、カイ2乗分布に従います。
大事な事として、母平均が分からない場合は自由度を$-1$する必要があるんでした。
ですので、自由度$k=4$の有意水準5%の%点を求めます。
カイ二乗分布表
| 0.025 | 0.05 | 0.95 | 0.975 | |
| 4 | 0.48 | 0.71 | 9.49 | 11.14 |
今回は上側検定ですので、「0.95」に対応する値をみると、$9.49$という事が分かりました。
帰無仮説が正しいか検証
結果をまとめると、
- 検定統計量$V=15.44$
- 境界値:$9.49$
です。
今回の結果は、棄却域に含まれる事が分かりました。
$9.49 < V(15.44)$
ですので、帰無仮説が棄却され対立仮説が採択されます。
- 対立仮説:$\sigma > 50$…採択
例題
以下のカイ2乗分布表を使って各問いに答えなさい。
カイ2乗分布表
| 0.005 | 0.025 | 0.05 | 0.95 | 0.975 | 0.995 | |
| 1 | 0.00 | 0.00 | 0.00 | 3.84 | 5.02 | 7.88 |
| 2 | 0.01 | 0.05 | 0.10 | 5.99 | 7.38 | 10.60 |
| 3 | 0.07 | 0.22 | 0.35 | 7.81 | 9.35 | 12.84 |
| 4 | 0.21 | 0.48 | 0.71 | 9.49 | 11.14 | 14.86 |
| 5 | 0.41 | 0.83 | 1.15 | 11.07 | 12.83 | 16.75 |
| 6 | 0.68 | 1.24 | 1.64 | 12.59 | 14.45 | 18.55 |
| 7 | 0.99 | 1.69 | 2.17 | 14.07 | 16.01 | 20.28 |
| 8 | 1.34 | 2.18 | 2.73 | 15.51 | 17.53 | 21.95 |
| 9 | 1.73 | 2.70 | 3.33 | 16.92 | 19.02 | 23.59 |
| 10 | 2.16 | 3.25 | 3.94 | 18.31 | 20.48 | 25.19 |
①
答え:$\sigma^2=4$
①まずは帰無仮説と対立仮説です。
- 帰無仮説:$\sigma^2=4$
- 対立仮説:$\sigma^2\neq4$
②続いて検定統計量を求めます。
問題文から、母平均は$μ=50$という事が分かっています。
$V=\frac{(48-50)^2+(50-50)^2+(51-50)^2+(47-50)^2}{4}=3.5$
③棄却域の設定
自由度$4$、有意水準5%の両側検定ですので、カイ2乗分布表から対応する値を探します。
「0.48」、「11.14」という事が分かりました。
④帰無仮説が正しいか検証
- 検定統計量$V=3.5$
- 境界値:「$0.48$」「$11.14$」
上記の結果でしたので、帰無仮説は棄却されませんでした。
$\sigma^2=4$
②
答え:$\sigma^2\neq4$
問題文から、母平均が分からない場合の検定だという事が分かります。
①帰無仮説と対立仮説
- 帰無仮説:$\sigma^2=4$
- 対立仮説:$\sigma^2\neq4$
②標本平均を求めてから検定統計量を求める
$\bar{X}=\frac{122+115+120+119+124}{5}=120$
$V=\frac{(122-120)^2+(115-120)^2+(120-120)^2+(119-120)^2+(124-120)^2}{4}=11.5$
③棄却域を設定
標本平均を使っているので、自由度は-1されて、$k=4$です。
また、有意水準5%の両側検定ですので、カイ2乗分布表から対応する値を探します。
「0.48」、「11.14」という事が分かりました。
④帰無仮説が正しいか検証
- 検定統計量$V=11.5$
- 境界値:「$0.48$」「$11.14$」
上記の結果、ギリギリですが棄却域に入りますので、帰無仮説が棄却され、対立仮説が採択されました。
$\sigma^2\neq4$
Work illustrations by Storyset