母分散既知の母平均の差の検定【0から始める統計検定2級講座㉛】

この講座の対象者は以下の方を想定しています。

この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。

今回は、母分散が分かっている場合の、2つの母集団の母平均の差の検定を行います。
前講座までの内容が頭に入っていれば、サクサク進められると思います。

分からない点があったら、しっかりと復習しながら進めましょう！

 

2つの母集団の平均の比較とは？

今回の講座で学ぶ事は、2つの母集団の平均の比較です。
これがどういった事かをまず説明します。

例えば、単純にA高校とB高校をそれぞれ母集団と見立て身長の平均を比較したり、畑を2つの区画にわけ、一方には肥料を与え、もう一方には何も与えないで成長率を比較したりする事です。

 

ビジネスシーンでも良く使われる

例えば、ECサイトの商品説明文を2つ用意し、どちらの方が購入率が高いかの比較であったり、A店舗とB店舗で別のイベントを行い、どちらの方がより集客人数があったかの比較など、本当に幅広いシーンで使われます。

 

 

母平均の差の検定の種類

今まで、母平均の仮説検定などでは、母分散が分かっている場合・分からない場合で2通りの求め方がありました。

しかし、母平均の差の検定の場合は、以下の3種類の求め方があります。

このように、それぞれで求め方が違います。
今回の講座では「母分散が分かっている場合」に絞って説明します。

他の2つは、次回以降の講座で説明します。

 

母平均の差の検定方法(母分散既知)

ではさっそく、母平均の差の検定方法を見ていきましょう！
例題を基に解いていきます。

 

例題

まず、記号を以下の定義とします。

• X農家の母平均は$μ_X$、標本平均は$\bar{X}$、母分散は$\sigma_X^2$、自由度は$m$
• Y農家の母平均は$μ_Y$、標本平均は$\bar{Y}$、母分散は$\sigma_Y^2$、自由度は$n$

 

また、解き方の流れとしては、仮説検定おなじみの以下の流れで行います。

 

①帰無仮説と対立仮説を立てる

まずは、2つの母平均が等しいものと仮定していきます。
ですので、帰無仮説と対立仮説は以下のようになります。

 

②検定統計量を求める

検定統計量$Z$を求めるには以下の式から求める事ができます。
今までに比べて複雑になっていますが、これを覚えないと問題を解く事ができませんのでしっかりと覚えましょう！

 

この式に代入するため、問題文を以下のように整理します。

また、現在の情報では$(μ_X-μ_Y)$の部分が分かっていませんが、帰無仮説$μ_X=μ_Y$より、同じ数字から同じ数字を引いているので、$0$になります。

では、それぞれの値を代入していきましょう。

 

$Z=\frac{15-18-0}{\sqrt{\frac{4}{10}+\frac{9}{10}}}=-0.263$

 

検定統計量$Z$は$-0.263$という事が分かりました。

 

③棄却域の設定

母平均の差の検定では何分布に従うのかが重要ですよね？

結論を言ってしまうと、確率変数$Z$は、帰無仮説が正しいとすれば、標準正規分布に従うのです。

また、問題文から有意水準は5%という事が分かっています。
そして、対立仮説$μ_X \neq μ_Y$なので両側検定になります。

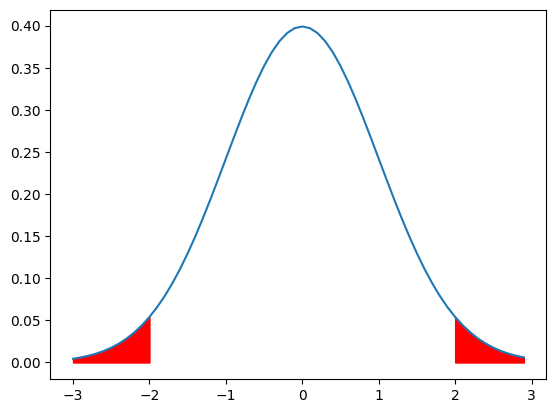
上記のように、左右0.025が棄却域になります。
ではその%点がいくつかというと、$0.5-0.025=0.475$となる値を標準正規分布表から見つけてくれば良いのですが、この値は$±1.96$であるという事はやってきましたね！
(統計検定2級を受けるならこの値はしっかり覚えておきましょう！)

このようにして、境界値は$±1.96$という事が分かりました。

 

④帰無仮説が正しいか検証

ここまでの情報を整理すると、

です。
上記の結果から棄却域には含まれないので、帰無仮説は棄却されません。

X農家とY農家のイチゴの重量の平均値に、有意に差があるとは言えませんでした。

 

 

あくまで母分散既知の求め方

この解き方はあくまで母分散が分かっている場合限定です。
次回以降に、母分散が分からない場合の解き方講座に移っていきますが、その為にはF分布を理解する必要があります。

一歩ずつ着実に学んでいきましょう！

 

練習問題

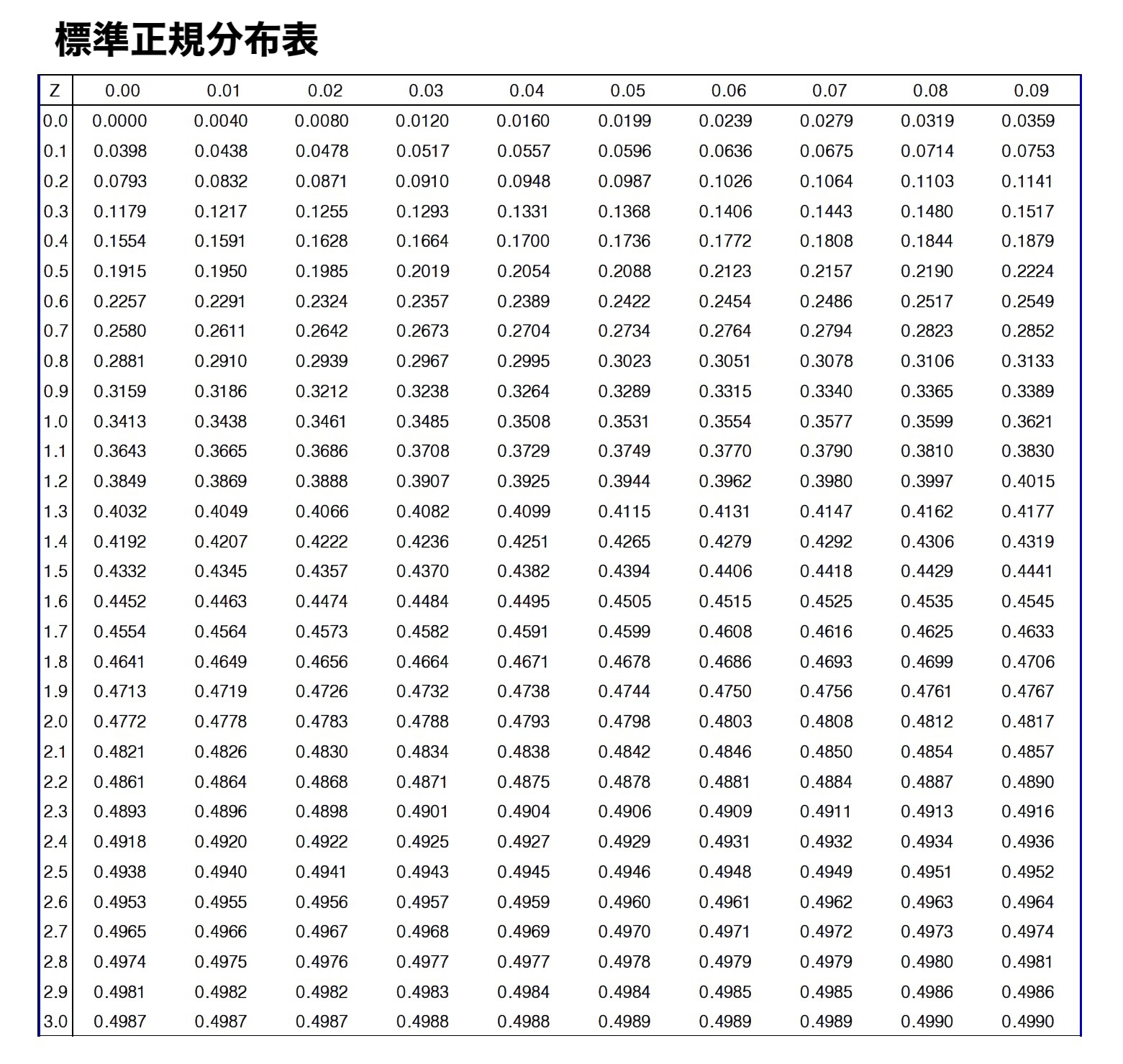
以下の標準正規分布表を使って練習問題をときなさい。

標準正規分布表

 

練習問題①

①

 

 

 

Work illustrations by Storyset