母比率の検定とは？【0から始める統計検定2級講座㉞】

この講座の対象者は以下の方を想定しています。

この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。

今回は、母比率の検定方法について解説します。
これまでに、母平均や母分散の検定をやってきましたが、今回は母比率についてです。
ビジネスシーンでもよく使われる検定ですので、統計検定だけでなく、その後も使える知識ですので、しっかりと覚えていきましょう！

 

母比率に関する検定とは？

母比率に関する検定とは何をするものなのかというと、母集団の中から標本を抽出し、そこから得た比率を母集団の比率として良いのかどうかを検定することです。

 

母比率の検定の例

例えば、以下の様なパターンがあります。

• ジャンケンを100回したところ、70回勝利した。勝率は0.5より大きいと言えるか？
• ある洗剤が「除菌率99%」と宣伝して販売されていた。実際に、100本購入し除菌率を調べたら90%であった。この宣伝は正しいと言えるか？

このように、標本の結果から、母集団の割合を検定することです。

ビジネスシーンでも、実際に聞いていた話しを母比率検定したら実は違っていた。
あるECサイトの施策の効果を母比率検定で評価する。
など、様々なシーンで活躍する検定です。

 

 

母比率の検定の流れ

では実際に母比率の検定の流れを見ていきましょう。

 

例題

では以下の例題を基に実際に解き方を見ていきましょう。

 

①帰無仮説と対立仮説を立てる

このようになります。
ちなみに$p$は母比率のことです。

 

②検定統計量を求める

検定統計量$Z$を求めるには以下の式から求める事ができます。

 

ちなみに$\frac{X}{n}$は標本比率の事です。
今回は、500人訪れた中の125人ですので、$\frac{125}{500}=0.25$となります。

その他の値もまとめると↓になります。

これを上記の式に代入して計算します。

$Z=\frac{\frac{X}{n}-p}{\sqrt{\frac{p(1-p)}{n}}}=\frac{0.25-0.2}{\sqrt{\frac{0.2(1-0.2)}{500}}}=\frac{0.05}{0.01789}=2.79$

 

このようにして、検定統計量$Z=2.79$という事が分かりました。
式は複雑そうに見えますが、計算する事はシンプルですので簡単です。

 

③棄却域の設定

何の分布に従うかというと、検定統計量$Z$は標準正規分布$N(0, 1^2)$にしたがいます。
また、両側検定なので左右2.5%点になるのですが、標準正規分布の2.5%点は$1.96$と$-1.96$でしたね。
この値が境界値となります。

 

 

④帰無仮説が正しいか検証

今までの結果をまとめると、

です。
検定統計量が棄却域に含まれるため、帰無仮説は棄却されます。
対立仮説の$p \neq 0.2$が採択されました。

よって、「商品紹介文の改善により変化があったと言える」ことが分かりました。

 

 

母比率の検定の練習問題

では最後に練習問題にチャレンジして、理解しているか確認しましょう！
以下の標準正規分布表を使って、解いていきましょう。

 

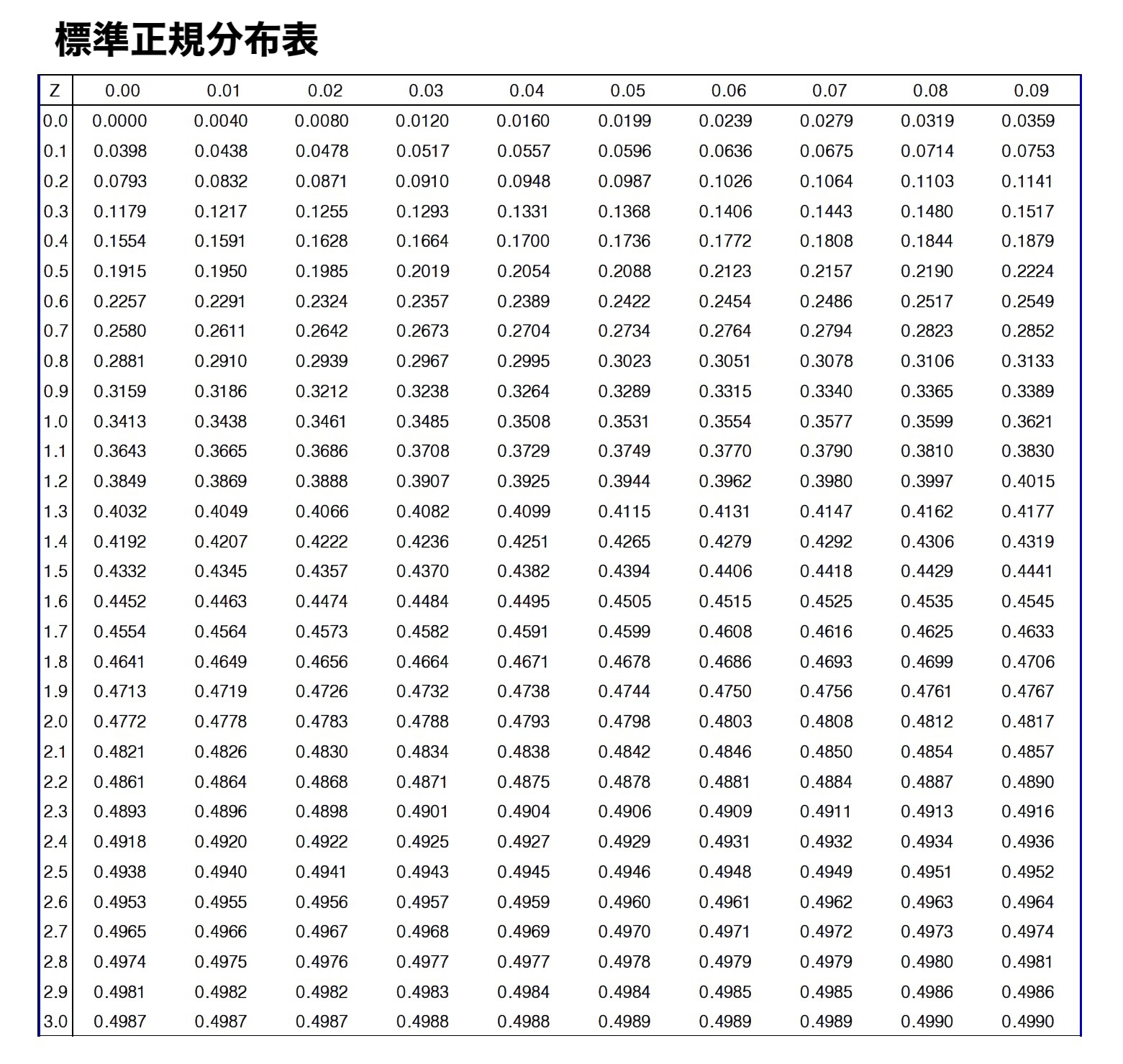
練習問題①

 

 

 

Work illustrations by Storyset