この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 連続型の確率変数ってなに?
- 確率密度関数の積分ってどうやるの?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回は、連続型の確率変数です。これが理解出来ないと、今後出てくる統計的推定の意味が理解できなくなるかも知れません。
しっかりと学習していきましょう。
連続型確率変数とは
まず、確率変数には離散型確率変数と連続型確率変数があります。
その意味を理解しましょう。
離散型確率変数
離散型確率変数は今までに出てきたサイコロやコインの表裏など、飛び飛びの値をとるものです。
サイコロでは[1, 2, 3, 4, 5, 6]のどれかの値を必ずとります。
1.5や4.52などの中途半端な値を取ることは絶対にないですよね?
このように、値がしっかりと離れているものが離散型確率変数です。
連続型確率変数
逆に連続型確率変数は、身長の170.234cmであったり、時間の15時00分30秒コンマ21…のように、連続する値の事です。
これらは飛び飛びの値をとらず、精密に測ろうとするときりがありません。
そのため、取りうる値に関しては範囲指定をする必要があります。
身長170cmという指定方法はだめで、170cm~180cmのように、範囲指定が必要です。
例えば、170cm~180cmを指定する場合は↓のように指定します。
$P(170\leqq X\leqq180)$
これは、$X$が170以上180以下の値をとる確率を表しています。
例えば、
荷物の配送時間を18:00~18:30の間に指定した。
この荷物の配達が18:00~18:15分の間に来る確率をもとめよ。
この問題は下記の式で表す事ができます。
$P(a \leqq X \leqq b)=\frac{b-a}{30}$
$P(0 \leqq X \leqq 15)=\frac{15-0}{30}=\frac{1}{2}$
このようにして、$\frac{1}{2}$と求める事ができます。
連続型確率変数の確率分布
離散型と違い、連続型確率変数の場合は$X$の取りうる値が無限にあることは話しましたね。
そのため、↓のように離散型の確率分布を表にすることはできません。
| $X$ | 1 | 2 | 3 | 4 | 5 | 6 |
| $p$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
連続型確率変数の場合はグラフで表します。
連続型確率変数のグラフ
先ほどの例題をグラフにすると↓のようになります。
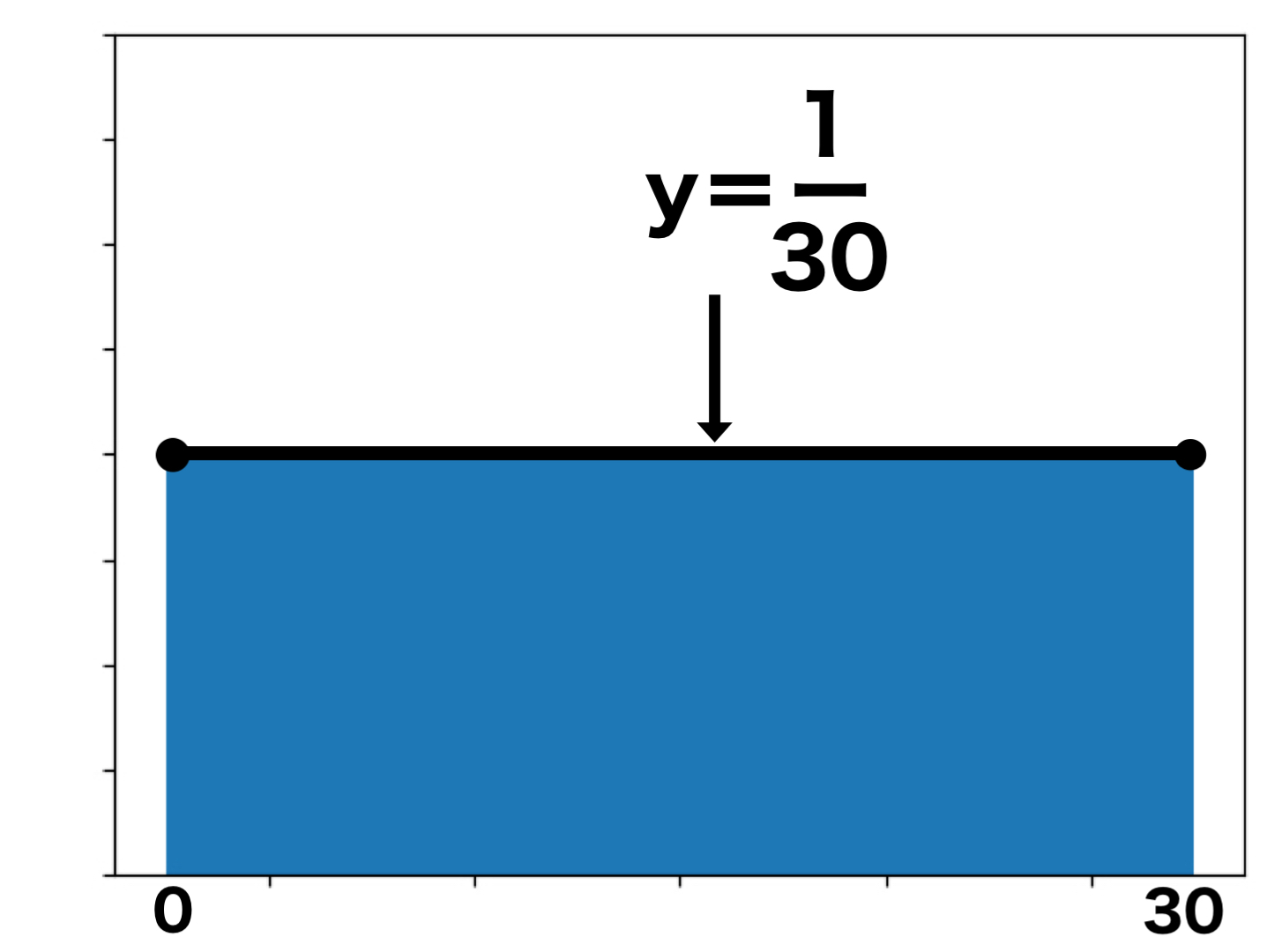
この確率分布表は、0分~30分の間に配達がくる確率を表しています。
来る確率はどの時間も均等です。
$X$の値は$0 \leqq X \leqq 30$ですので、上記の$X$軸は0~30を表しています。
そして、大事なポイントとして、青の面積は「1」になります。
そのため、縦軸である$y$軸の点は$\frac{1}{30}$となります。
このように、確率を面積にする事は非常に重要です。
そうする事が、様々なケースでの確率を求めやすくする事ができます。
例えば、先ほどの例題もグラフの面積を求める事で確率を知る事ができます。
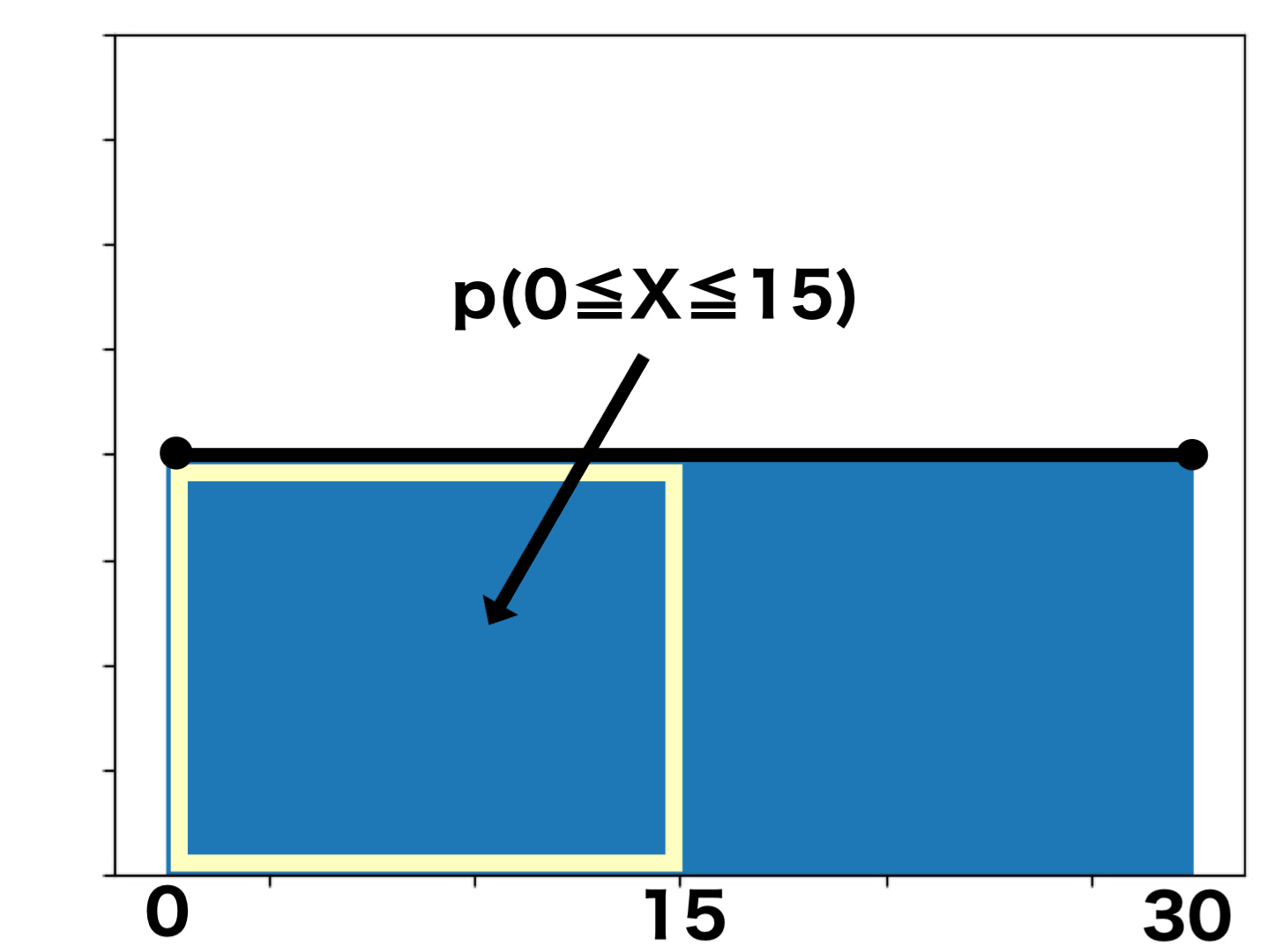
黄色い線の枠内が、0分から15分の間に来る確率です。
まさに長方形の形をしているので、縦×横をする事で面積を求められます。
- 縦:$\frac{1}{30}$
- 横:$15-0=15$
$\frac{1}{30}×15=\frac{1}{2}$
このようにして、$\frac{1}{2}$と求められます。
確率密度関数とは?
まず関数と聞いて皆さんは何か分かるでしょうか?
エクセルを知っている人なら色々な関数を知っている人も多いと思います。
数学における関数を簡単に説明すると、関数は入力値を対応する出力値に変換する機械だとイメージしてください。
例えば、関数は$f(x)$で表される事が多く、$f(x)=x^2$という関数があります。
この関数の$x$に$2$を入れると2乗されて、$4$になって返ってきます。
これが数学における関数です。
では先ほどのグラフの式を関数で表すと↓の様になります。
\begin{equation}
f(x)=
\left\{
\begin{alignedat}{2}
\frac{1}{30} \quad (0\leqq X \leqq 30) \\
0 \quad (x<0, x>30)
\end{alignedat}
\right.
\end{equation}
これを、確率密度関数と言います。
例えば、$X$の値が$a \leqq X \leqq b$の確率密度関数をグラフで表すと↓の様になります。
上で見た確率が一定の一様分布と違い、曲線になっています。
確率密度関数によっては、山なりになったり直線になったりと様々です。
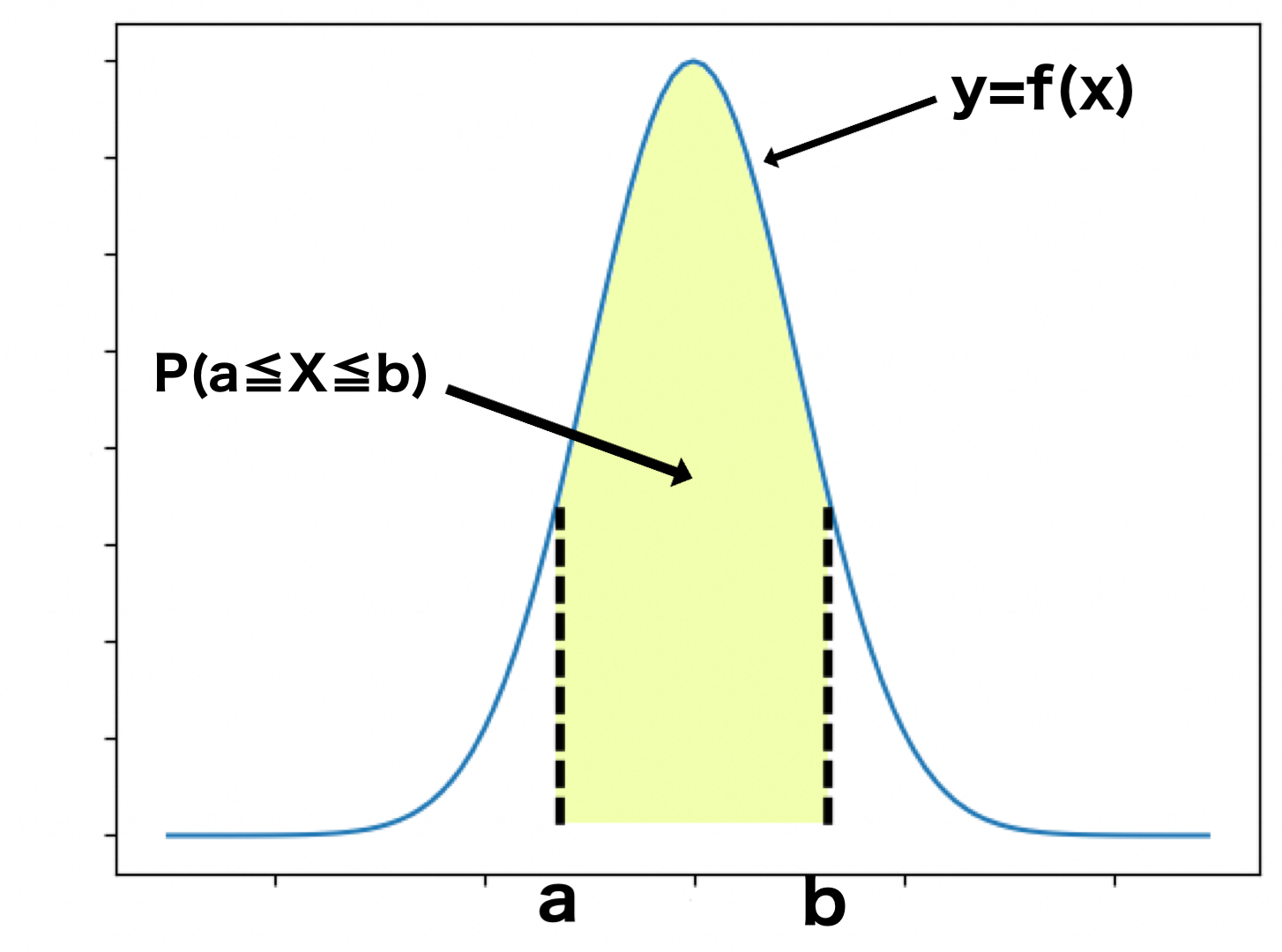
黄色い部分が確率$P(a \leqq X \leqq b)$です。
確率密度関数が$f(x)=-0.5x+2$の場合は↓のような右下がりの直線になります。
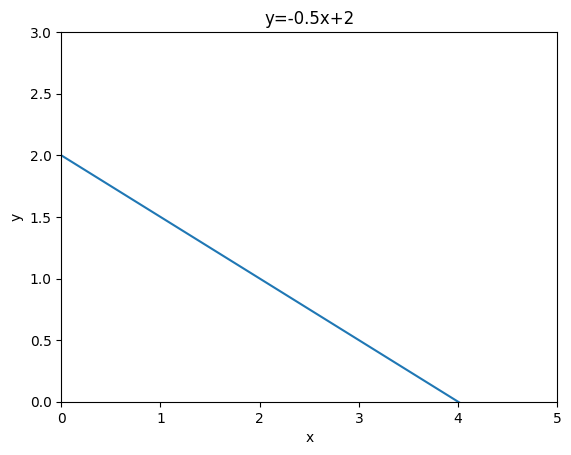
確率密度関数の概要
確率密度関数の押さえておきたいポイントしては、以下の2点があります。
- 全体の面積は1
- ちょうどの確率は0
「全体の面積は1」ですが、↓のグラフのように、$X$の最小値を$a$、最大値を$b$とすると、$P(a \leqq X \leqq b)=1$となります。
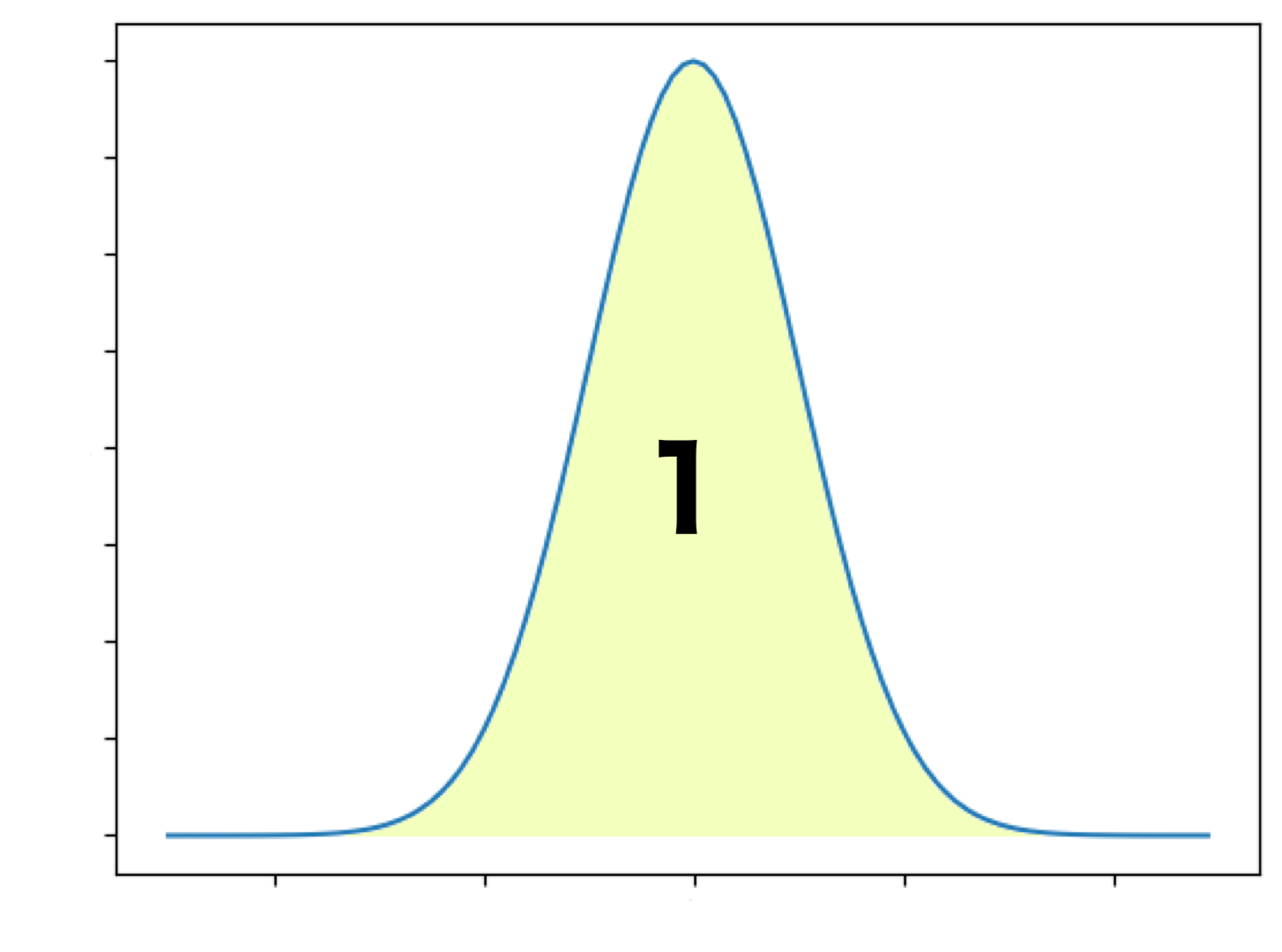
また「ちょうどの確率は0」ですが、離散型のサイコロの例の場合はちょうど1の目がでる確率は$\frac{1}{6}$でした。
しかし、連続型確率変数の場合はまったく違い、0になってしまうのです。
先ほどの配達時間の例題で、6:15分ちょうどの確率を求めようと思っても、この場合は範囲指定をされていないため面積は0です。
連続型確率変数の確率は面積で求める!
この原則をしっかりと押さえておきましょう。
グラフが曲線の場合の確率密度関数
確率は面積で求めると言っても、上記のように曲線の場合はどのように求めれば良いのか?という問題が出てきますよね?
直線の倍は、三角形や四角形の形にして求める事ができましたが曲線の場合はそうもいきません。
そんな時は積分で求めます
「積分は苦手~」という方も多いかもしれませんが、統計で必要な知識は簡単です。
概念だけ理解出来れば十分ですので安心してください。
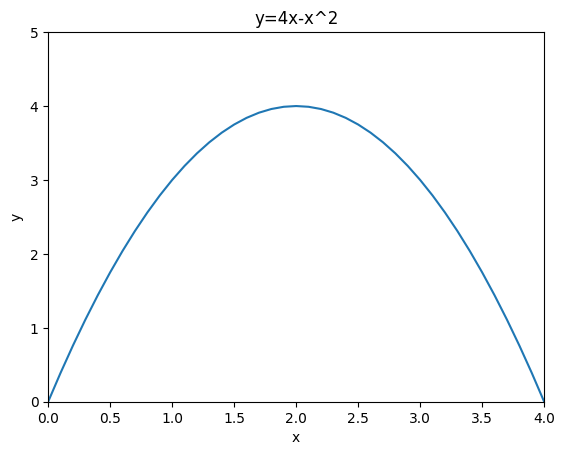
例えば、↓のように$y=4x-x^2$の確率密度関数があります。
この場合に確率$P(1 \leqq X \leqq 3)$を求めてみましょう。
まずはどのように求めるのか?考え方の説明をします。
まず、$x$が1から3の範囲に、↓のように長方形を敷き詰めます。
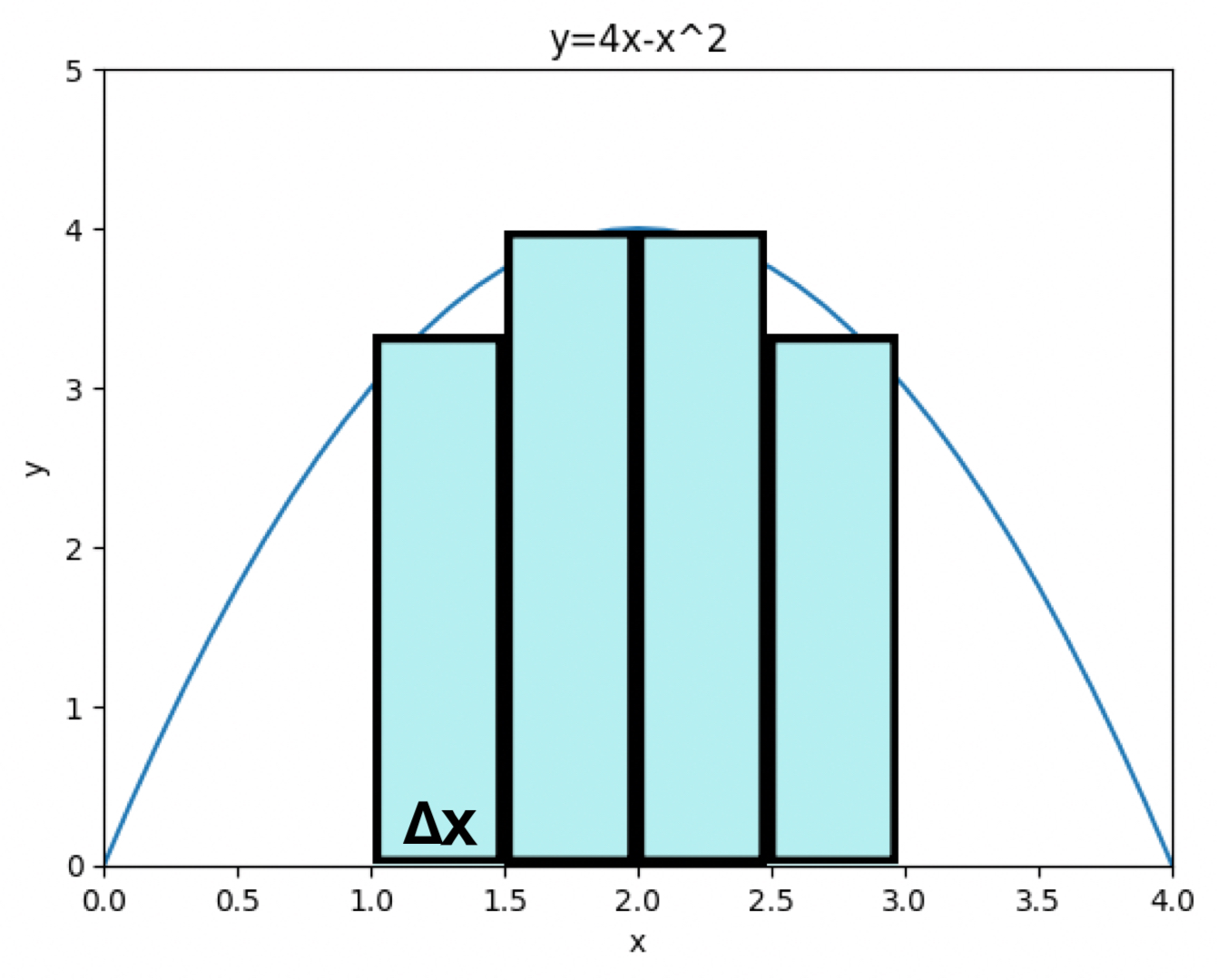
アバウトですが、このように長方形を敷き詰め、各長方形の面積を求めます。
それからその面積を全て足し合わせる事で、指定の区間の確率を求める事ができるのです。
長方形の面積を求めるには縦×横ですね。
長方形の横幅は$\Delta x$(デルタ)とします。
また高さは$y$である$f(x_1),f(x_2),…$です。
つまり、
$\Delta x×f(x_1)+\Delta x×f(x_2)+…$
このように計算していけば良いのです。
基本的にはこのように、長方形の面積を求めて足し合わせることで、指定の範囲の確率を求める事ができるのです。
でも本当にそれで良いのか不安ですよね?
上記の長方形だとあまりにもアバウトだと感じると思います。
長方形をより細かくしよう
そんな時はより細かい長方形を敷き詰めましょう。
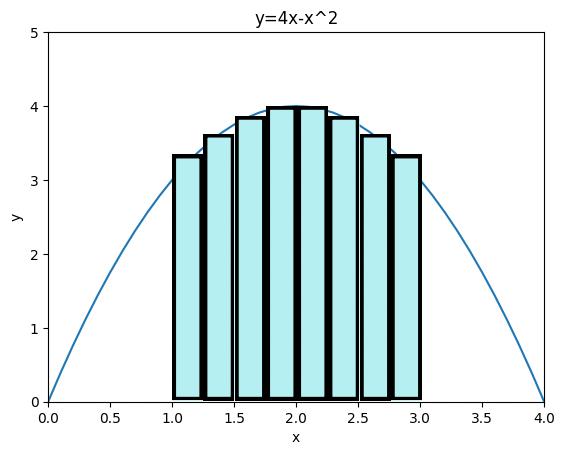
このように、$\Delta x$の幅を小さくし、細かい長方形を敷き詰めることでよりなだらかになったと思います。
これでもまだ不十分ですので、より小さくしていけばどんどんなだらかになっていくと思います。
そして、$\Delta x$を限りなく0に近づければ、求める面積に限りなく等しくなると思います。
イメージとしては、上記の$\Delta x$は0.5ですが、これを0.00000000000001やそれ以上に小さくすると非常に滑らかな曲線になります。
このように、
$\Delta x$を限りなく0に近づけ、求める面積に限りなく等しくする積分の考え方を求積法と言います。
ちなみに、限りなく0に近い$\Delta x$を$dx$と書くので覚えておきましょう。
積分の式
$dx$を使って、積分の式を書くと↓になります。
$\int_{a}^{b} f(x)dx$
また新しい記号が出てきましたね~!
意味は簡単ですので安心してください。
- $\int$:全てを足し合わせるという意味です。
- $\int_{a}^{b}$:aからbまで足し合わせます。つまり$P(a \leqq X \leqq b)$の確率を足し合わせて求めます。
このように、連続型確率変数$X$が$a \leqq X \leqq b$の値を取る確率$P(a \leqq X \leqq b)$は、積分記号を使い↓のように表します。
$P(a \leqq X \leqq b)=\int_{a}^{b} f(x)dx$
例題
↓の確率密度関数があるとき、$2 \leqq X \leqq 3$となる確率はいくらでしょうか?
\begin{equation}
f(x)=
\left\{
\begin{alignedat}{2}
\frac{1}{5} \quad (0\leqq X \leqq 5) \\
0 \quad (x<0, x>5)
\end{alignedat}
\right.
\end{equation}
まずこの確率密度関数の2行目の$0(x<0,x>5)$の意味ですが、$x$が0より小さくなったり、5より大きくなる確率は0である事を示しています。
これをプロットすると↓になります。
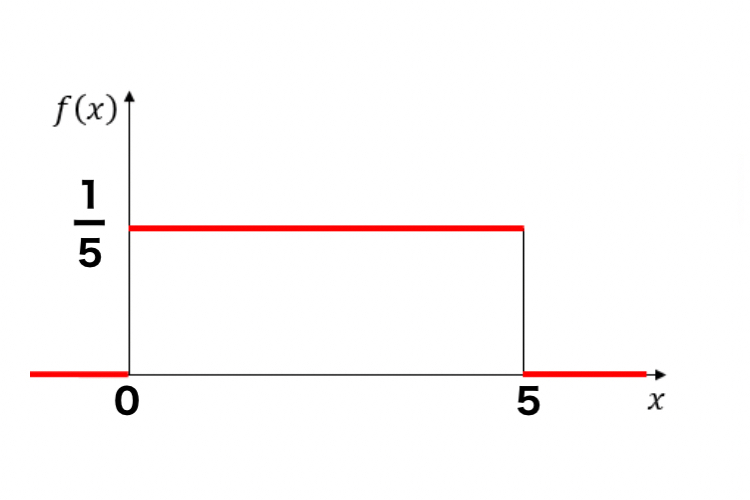
今回は、$2 \leqq X \leqq 3$となる確率を求めよとあるので、↓の図の青い部分の面積を求めます。
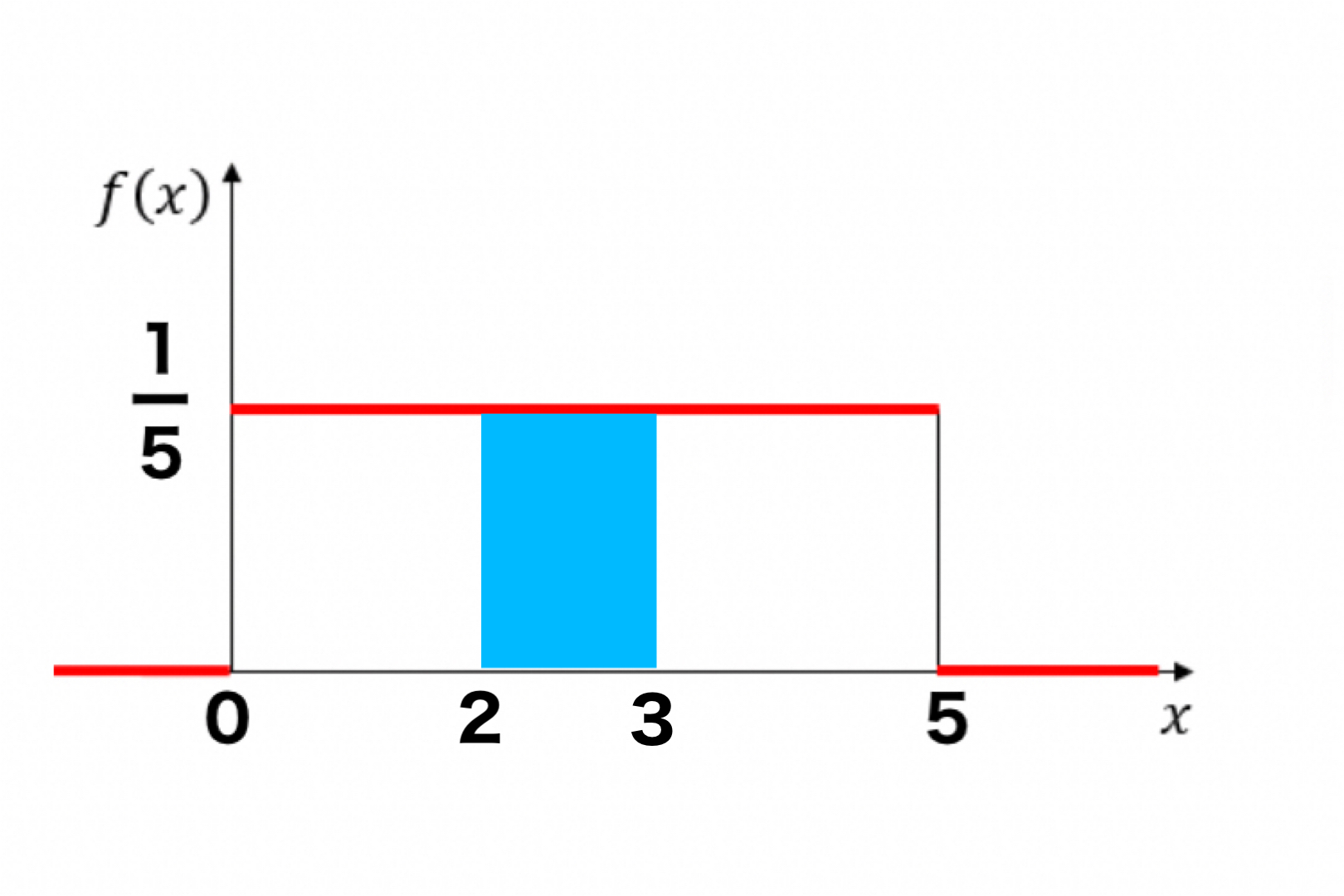
これは、積分の式を使って求めます。
$P(2 \leqq X \leqq 3)=\int_{2}^{3}f(x)dx$
これを解けば良いのですが初見ですと何が何だか分からないですよね?
でもやる事は非常に簡単ですので、一つずつ見ていきましょう。
まずは$f(x)$に確率密度関数である$\frac{1}{5}$を代入します。
$=\int_{2}^{3}\frac{1}{5}dx$
次に$\int$(インテグラル)を外すのですが、ついでに$dx$の$d$も外れ、↓になります。
$=[\frac{1}{5}x]_{2}^{3}$
この式の計算方法としては、$x$に3を代入して$\frac{1}{5}$を掛けた数字から2を代入した数字を引けば良いのです。
なぜこの様な計算をするかというと、もう一度↑の図の青い面積を見てください。
この面積を求めるには0~3までの面積から0~2までの面積を引けば、青い部分だけ残りますよね?
それを行っているのです。
$\frac{3}{5}-\frac{2}{5}=\frac{1}{5}$
この様にして、青い部分の面積は$\frac{1}{5}$と求める事ができました。
連続型確率変数の期待値と分散
連続型確率変数$X$の取りうる値の範囲を$α \leqq X \leqq β$とすると、期待値と分散は↓になります。
- $E(X)=\int_{α}^{β} xf(x)dx$
- $V(X)=\int_{α}^{β} (x-μ)^2f(x)dx$
ただし$μ=E(X)$
練習問題
①
答え:$\frac{1}{2}$
まず$f(x)$確率密度関数が分かっていないので、求めましょう。
$f(x)=a$として考えます。
確率の総和は1であることから、↓の式で求める事ができます。
$1=\int_{0}^{4} f(x)dx=\int_{0}^{4} adx$
$=[ax]_{0}^{4}=a×4-a×0=4a$
$4a=1$
$a=\frac{1}{4}$
この様にして確率密度関数を求める事ができました。
まとめると、↓になります。
\begin{equation}
f(x)=
\left\{
\begin{alignedat}{2}
\frac{1}{4} \quad (0\leqq X \leqq 4) \\
0 \quad (x<0, x>4)
\end{alignedat}
\right.
\end{equation}
確率密度関数を$f(x)$に代入して計算すると、答えが出ます。
$P(2\leqq X \leqq 4)=\int_{2}^{4} \frac{1}{4}dx$
$=[\frac{1}{4}]_{2}^{4}$
$=\frac{1}{4}×4-\frac{1}{4}×2$
$=\frac{2}{4}=\frac{1}{2}$














