この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 標準正規分布表ってなに?
- 上側、下側確率ってなんのこと?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回は正規分布に一歩踏み込んで、正規分布の確率計算と標準正規分布表の解説を行います。
標準正規分布表を使って確率を求める
今回は、正規分布に従う確率変数が、ある値をとる確率を求める方法を解説します。
どういう事かというと、以下のような問題を解けるようになるのです。
男性の平均身長が170cmで、標準偏差が7の正規分布に従うとき、身長185cm以上の男性の確率は何%か?
確率変数$X$は正規分布$N(170, 7^2)$に従います。
まずは何を求めれば良いのか理解するために、↓の図をみてみましょう。
平均170cmで標準偏差が7の場合の正規分布です。
この185cm以上の確率を求めるので、赤く塗られている部分の確率を今回は求めます。
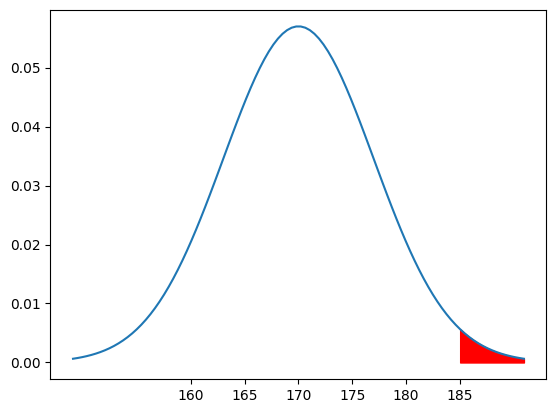
ちなみに175cm以上の場合は↓のように、一気に範囲が広くなります。
赤い範囲が広い方が確率が高くなるので、視覚からみても175cm以上に比べ、185cm以上というのは狭き門なのが分かります。
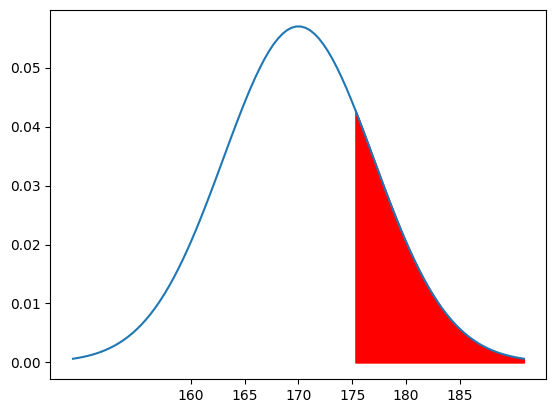
では、話しを戻しましてこの185cm以上の赤い部分の確率を求めるには、前回やった以下の積分の式を使えば求める事ができます。
\begin{equation}
f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}
\end{equation}
しかし、これを手計算で求める問題は統計検定2級では出ませんので安心してくださ。
実務で求めるとなっても何かしらのツールを使って求めます。
ではどうやって求めるかと言うと、標準正規分布表を使って求めます。
標準正規分布表とは何か?
下記の様な表の事を標準正規分布表と言います。
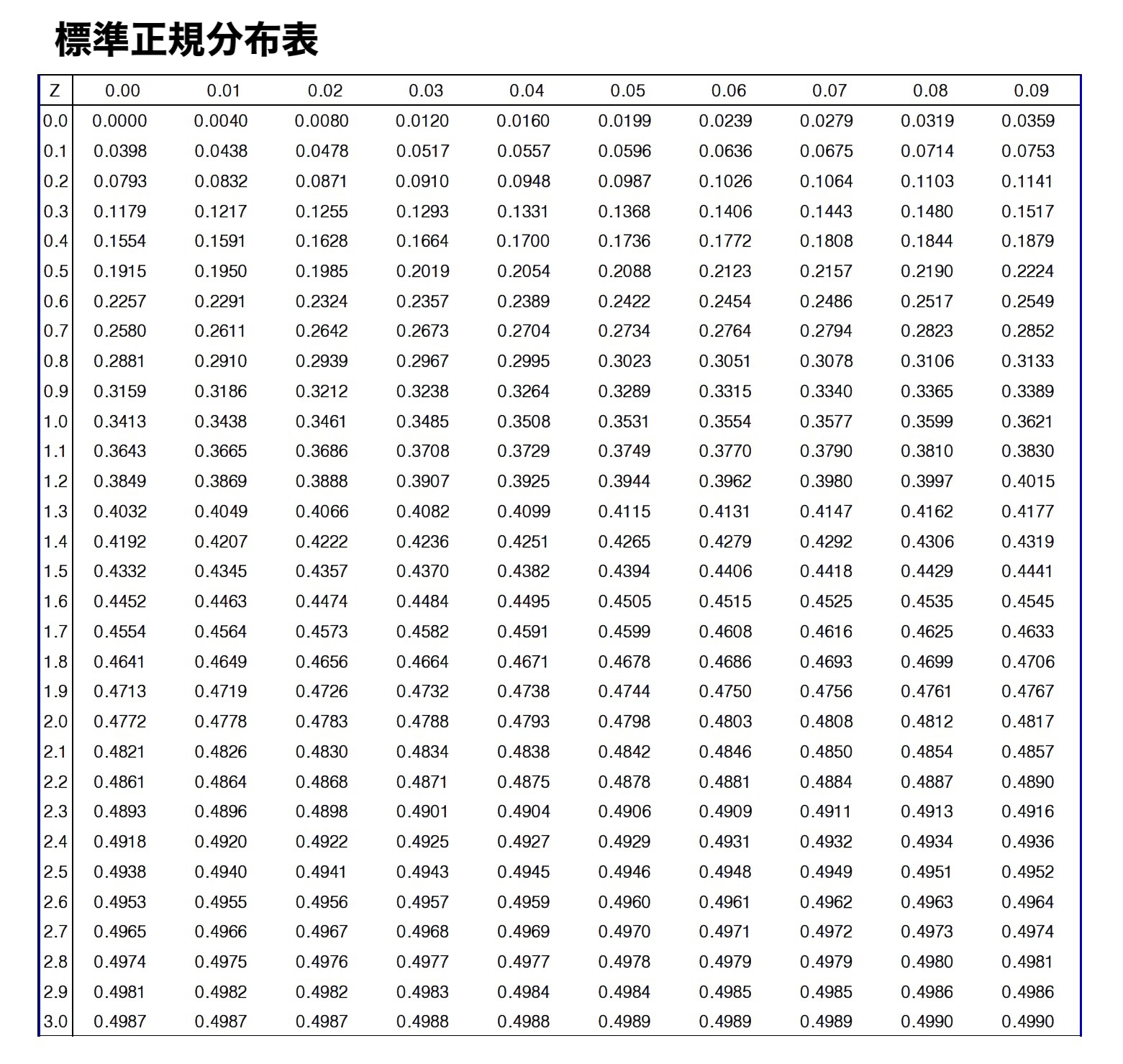
これを使うことで、先ほどの確率を求める事が出来るのです。
標準正規分布表を使った確率の求め方
男性の平均身長が170cmで、標準偏差が11の正規分布に従うとき、身長175cm以上の男性の確率は何%か?
では先ほどの例題を少し変化させ、実際に確率を求めてみましょう。
↓の図で見ると、175cm以上となる赤い部分の確率を求めるのです。
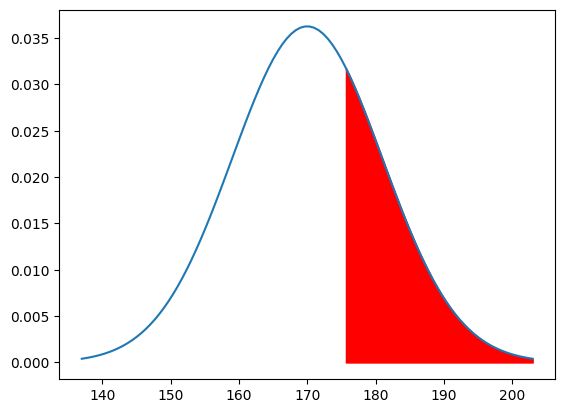
確率の求め方としては以下の流れで行います。
非常にシンプルです。
- 標準化する
- 標準正規分布表から対応する値を探す
- 上側、下側、両側確率のどれか判定する
- 計算
ではそれぞれの流れを見ていきましょう。
標準化する
まず、標準化する方法ですが、前回出てきた式を使って標準化を行います。
平均を0、分散を1にするや~つですね!
$Z=\frac{X-μ}{\sigma}$
今回は、
- $X=175$
- $μ=170$
- $\sigma=11$
ですので、これを式に当てはめて計算します。
$Z=\frac{175-170}{11}=0.454545..$
$Z$得点は約0.45だという事が分かりました。
図にすると、↓の赤い部分が0.45以上です。
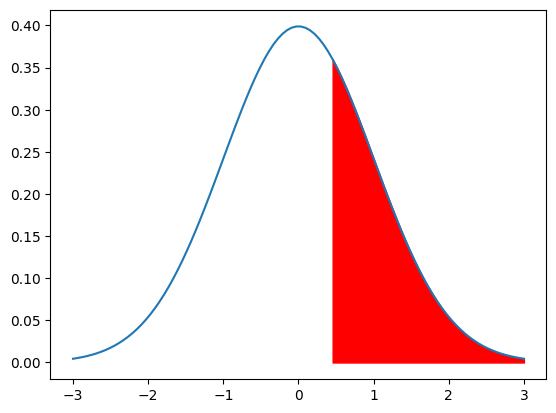
これで標準化する事ができたので、次は標準正規分布表を使います。
標準正規分布表から対応する値を探す
標準正規分布表には左端の行に少数点1桁までの数字があり、上端の列にはは少数点2桁までの数字が書いてあります。
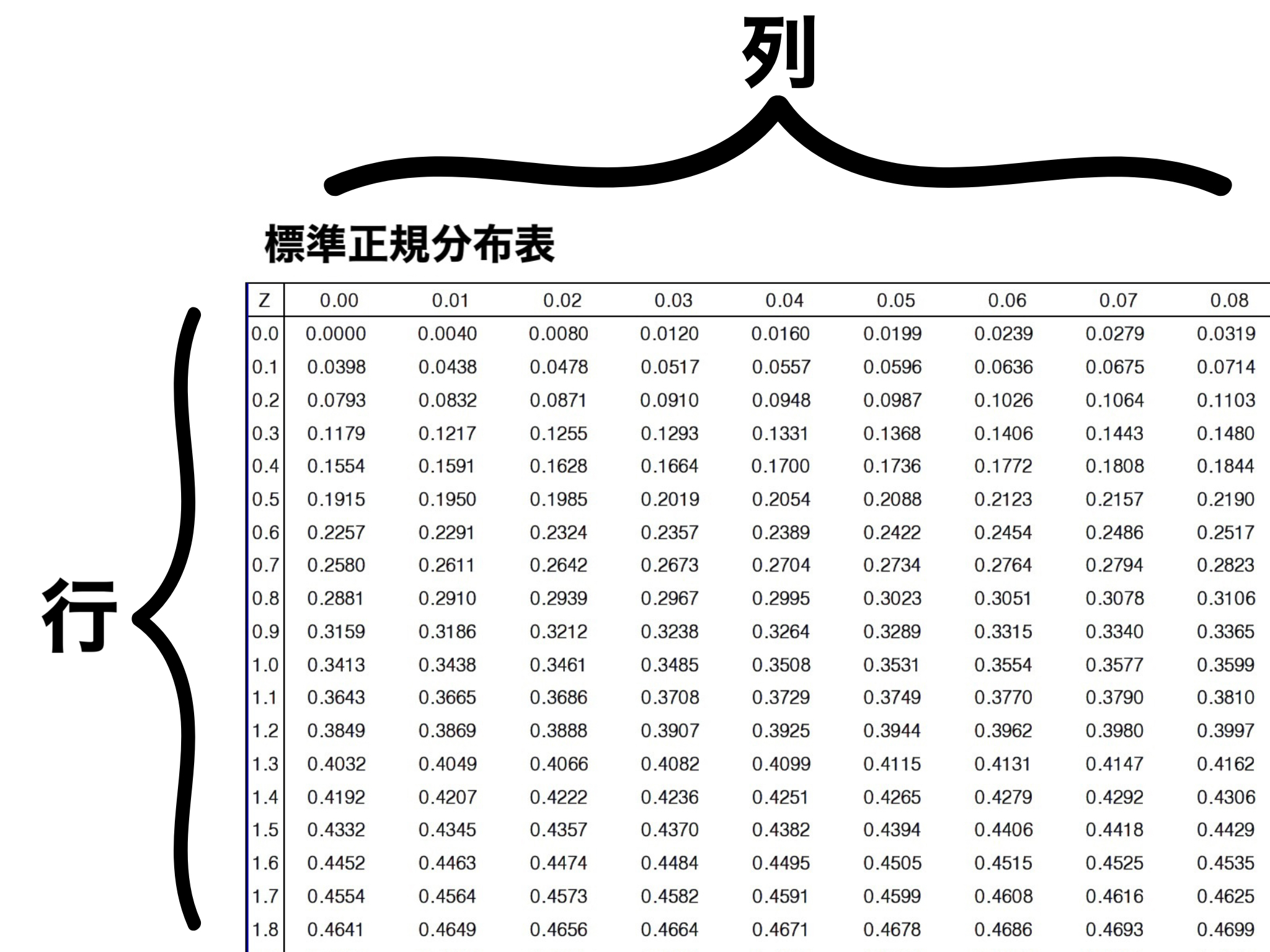
ここで先ほどの$Z$得点の0.45を使います。
少数点1桁目までの「0.4」の行と、少数点2桁目の「0.05」の列の交わる部分が対応する値です。
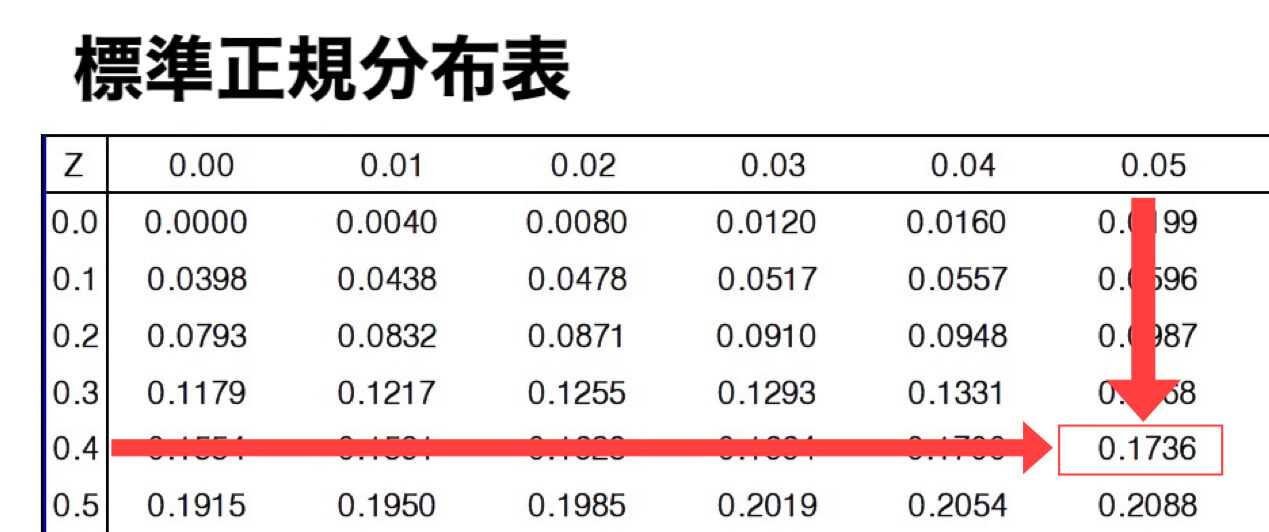
「0.1736」という事が分かりました!
ではこの数字が何を表しているのかが気になりますよね。
下の図の青い部分の確率です。
ようは、$P(0 \leqq Z \leqq 0.45)$、つまり平均0とした場合の0~0.45までの間の確率です。
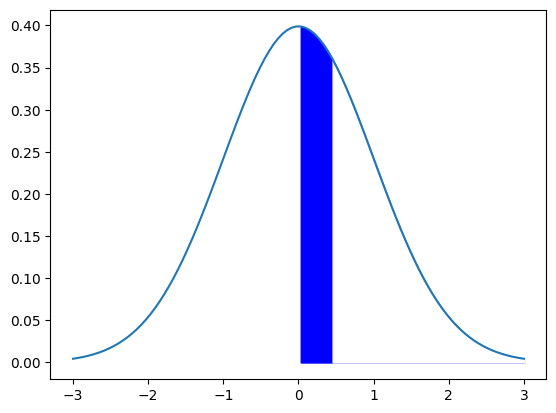
この青い部分の確率が「0.1736」なのです。
しかし、今回求めたいのは0~0.45までの間の確率ではなく、0.45以上の確率ですよね。
それを求めるためにもうひと手間かかります。
上側、下側、両側確率のどれか判定する
もう一度今回求める確率の図を見てみましょう。

今回の0175cm以上のように、~以上の確率を求めるのは上側確率と言います。
逆に「165cm以下の身長」のように、~以下の場合↓の図のようになります。
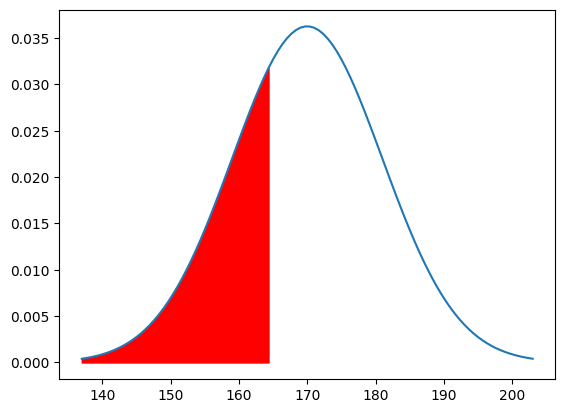
~以下の確率を求めるのは下側確率といいます。
そして、「165cm以下か175cm以上」のように、両方の確率を求めるのは両側確率と言います。
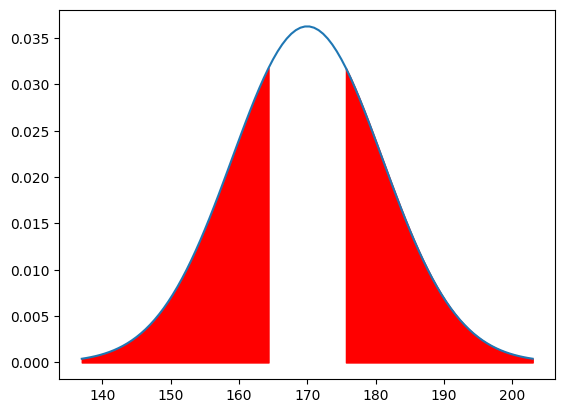
このように、今求めるべきなのは上側か?下側か?それとも両側なのかを知る必要があります。
今回のは「175cm以上」ですので、もちろん上側確率です。
計算する
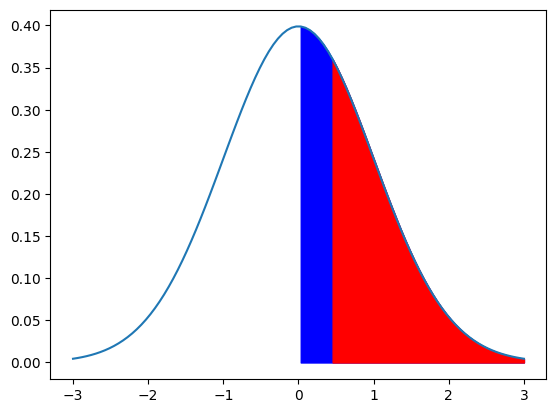
ここまでの情報を整理すると、
- $Z$値が$0.45$
- $P(0 \leqq Z \leqq 0.45)$の確率が$0.1736$。(青の面積)
となります。
つまり、あとは赤い部分の面積を求めれば、「身長175cm以上」の確率を求める事が出来るのです。
ではどの様にして求めるかと言うと、今回求めるのは上側確率であり、そもそも0以上となる確率は$0.5$となります。
これは確率の総和は1となるため、0を平均とした場合、プラスになる確率もマイナスになる確率もそれぞれ0.5となります。
ですので、上の図の赤と青を足した面積が0.5となるのです。
0.5から青の面積を引けば赤の面積を求める事ができますね!
$0.5-0.1736=0.3264$…答え
この様にして、175cm以上となる確率は$0.3264$だという事が分かります。
標準正規分布のいろいろな確率の求め方
さきほど、上側確率や下側確率、両側確率など出てきましたが、その点をもう少し深堀りさせてください。
それぞれの場合の求め方を解説します。
上側確率の求め方
標準正規分布(平均0、分散1)で、$1.96 \leqq X$になる確率を求めよ
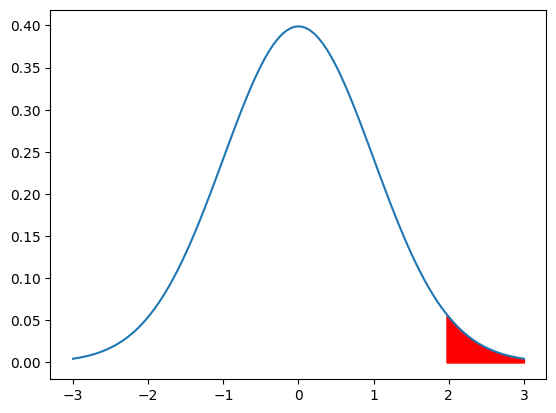
赤い面積が$1.96 \leqq X$になる確率です。
おさらいになりますが、上側確率の場合は下記の様に求めます。
まず、標準正規分布表の$1.96$に対応する値を探します。
今回は$0.4750$でした。
そして上側確率ですので、プラスになる確率の$0.5$から引けば良いのでした。
$0.5-0.4750=0.025$…答え
下側確率の求め方
標準正規分布(平均0、分散1)で、$X \leqq -1.96$になる確率を求めよ
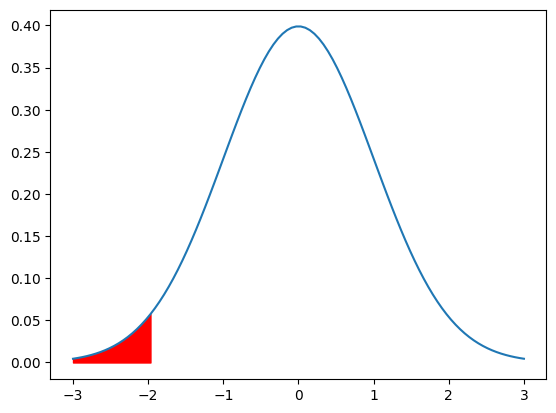
今度は下側確率です。
しかし、求め方は上側確率とほぼ一緒ですので非常に簡単です。
標準正規分布表から$-1.96$に対応する値を探せば良いのですが、標準正規分布表では絶対値で検索するので1.96と同じ、$0.4750$です。
そしてマイナス側の確率ももちろん$0.5$ですので、↓の式で求められます。
$0.5-0.4750=0.025$…答え
下側確率の変形
標準正規分布(平均0、分散1)で、$X \leqq 1.96$になる確率を求めよ
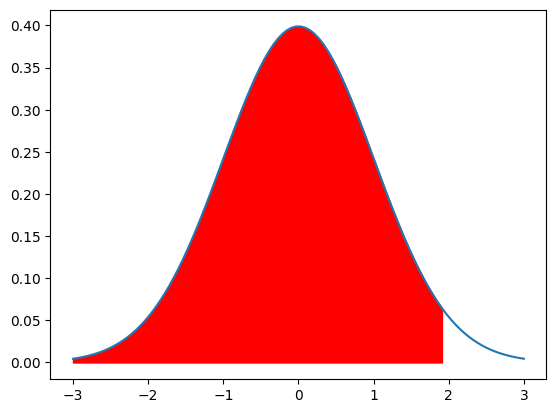
続いて、$1.96$以下になる全ての確率を求めます。
考え方が分かれば非常に簡単です。
まずは、$1.96$の確率を求めるのですが、既に$0.4750$という事が分かっていますね。
それにマイナス側の確率である$0.5$を足せば良いだけです。
$0.5+0.4750=0.975$…答え
両側確率の求め方
標準正規分布(平均0、分散1)で、$1.96 \leqq |X|$になる確率を求めよ
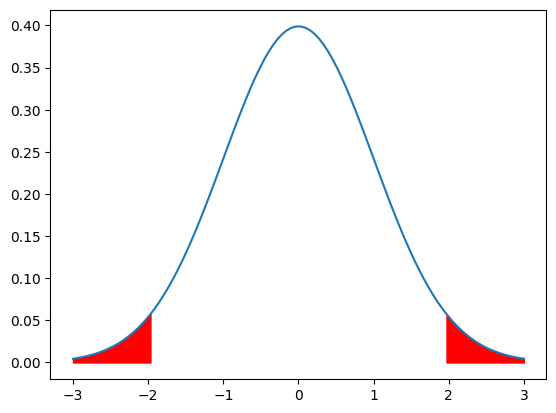
$|x|$というのは絶対値のことであり、確率変数の絶対値がある値以上になる確率を両側確率と言います。
ですので、今回の場合は上記の様に2箇所の赤い面積を足した値を求めます。
これも非常に単純で、片方の面積を求めれば正規分布は左右対象ですので、$×2$をすれば求める事ができます。
$0.025×2=0.05 $…答え
パーセント点を求める
今までは、「175cm以上」などと指定してきました。
しかし、「身長で日本の男性の上位5%に入るには何cm以上必要か?」
この様に、パーセントから求める場合もあります。
下の例題を基に考えていきましょう。
例題
男性の平均身長が172cmで、標準偏差が8の正規分布に従うとき、上位30%に入るには何cm以上必要か?
この様な問題の場合、まず上側なのか下側なのか、それとも両側なのかを確認します。
今回の場合は「上位」とありますので、上側を求める問題です。
まず、標準正規分布表から、上側30%点がいくつになるかを求めます。
上側確率$P(Z \leqq a)$が$0.3$なので、
$P(0 \leqq Z \leqq a)=0.5-0.3=0.2$
となります。
続いて標準正規分布表から、$0.2$に近い値を探すと、「0.1985」という事が分かります。
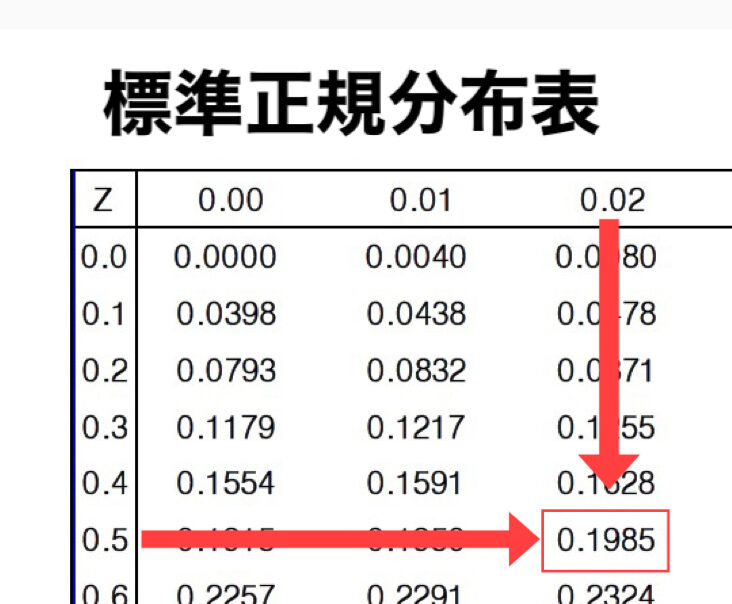
この時、行の値は$0.5$で列の値は$0.02$ですので、$a$の値は$0.52$となるのです。
次にやる事は、標準正規分布に従う確率変数$Z=0.52$を平均$172$、標準偏差$8$の正規分布にしたがう確率変数$X$に変換します。
あとは、前に下記の標準化の式を見た事があると思いますが、この式に代入して$X$の値を求めれば良いのです。
$Z=\frac{X-μ}{\sigma}$
このまま代入する前に、$X$を求めやすい様に変形させてから代入します。
$X=μ+\sigma Z$
この式に、
- $μ=172$
- $\sigma=8$
- $Z=0.52$
を代入します。
$X=172+8×0.52=176.16$…答え
以上から、身長176.16cm以上あれば、上位30%に入れる事が分かりました。(サンプルデータを使っているので、現実とは異なります。)
練習問題
①
答え:9.18%
まずは標準化します。
$Z=\frac{X-μ}{\sigma}=\frac{92-72}{15}$
$Z=1.3333….$
$Z$が$1.33$だと言う事が分かりました。
次に標準正規分布表から対応する値を探します。
すると「0.4082」という事が分かりました。
最後に、上側確率なので$0.5$から引けば答えがでます。
$0.5-0.4082=0.0918$
この様にして、A君の成績は上位9.18%と言う事が分かりました。
②
答え:56.64
まず、上側確率の「0.1(10%)」とありますので、標準正規分布表の$0.1$に対応する$Z$値を探したくなりますがこれは間違いです。$0.5$で引かなければいけません。
$0.5-0.1=0.4$
$0.4$に対応する値を標準正規分布表から探すと、$1.28$だと言う事がわかります。
後は標準化の式に当てはめて考えます。
$\frac{X-μ}{\sigma}$
$\frac{72-μ}{12}=1.28$
$μ=56.64$
平均点は$56.64$だという事が分かりました。














