正規分布と標準偏差の性質【0から始める統計検定2級講座⑰】

この講座の対象者は以下の方を想定しています。

この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。

今回は正規分布と標準偏差について、それぞれの性質をさらに深堀りしていきます。

 

平均と標準偏差の関係

いきなり正規分布の性質として大事な事を言います。

このような性質を持っているのです。

 

どういう事かというと、あるテストの平均点が70点で、標準偏差が10だとします。
そうすると、下記のことが言えるのです。

• 60～80点の間に68.3%の生徒が収まる
• 50～90点の間に95.4%の生徒が収まる
• 40～100点の間に99.7%の生徒が収まる

 

 

証明

では本当に上記の事が言えるのか？
なぜそうなるのかを計算して求めてみましょう。

標準正規分布分布表を使えばすぐに分かります。
標準正規分布表が良く分からないという方はコチラの講座をどうぞ！

 

まず、↑の証明をします。

正規分布を標準化した標準正規分布を考えてください。
これは平均が0で、標準偏差が1でしたね。

この場合、$P(-1 \leqq Z \leqq 1)$と表せます。
標準正規分布表から、$a=1.00$に対応する値を見ると、$0.3413$と言う事が分かります。

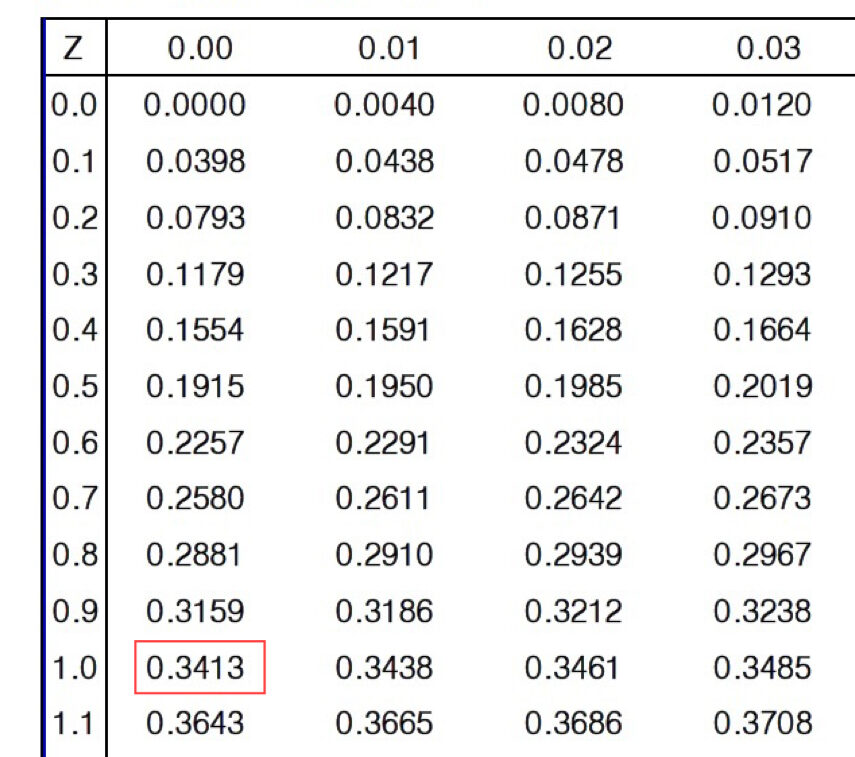
これは、$P(0 \leqq Z \leqq 1)$までの値であり、$P(-1 \leqq Z \leqq 0)$の値も求める必要がありますが、正規分布は左右対象ですので、単純に2倍すれば大丈夫です。

$0.3413×2=0.6826$…「平均±標準偏差」

 

このようにして、平均±標準偏差の範囲にデータの68.3%が入る事が分かりました。

 

同じようにして、「平均±標準偏差×2」の場合は$a=2.00$の値は$0.4772$です。
これを2倍すると、

$0.4772×2=0.9544$…「平均±標準偏差×2」

と、求める事ができます。

 

そして「平均±標準偏差×3」の場合は$a=3.00$の値は$0.4987$ですので、

$0.4987×2=0.9974$…「平均±標準偏差×3」

となります。

 

平均±標準偏差の面積

数字だけでは無く、視覚的にも見てみましょう。

 

「平均±標準偏差」

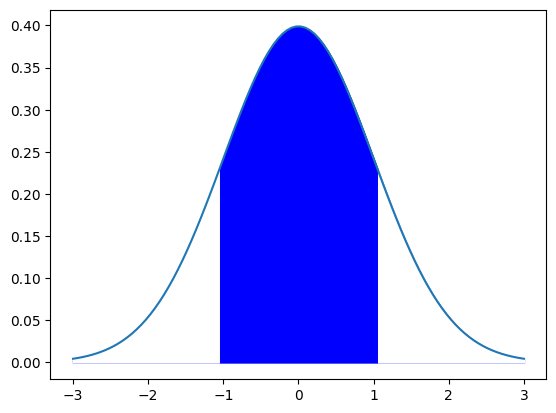
青い分部の面積が、平均±標準偏差の面積になります。

 

標準偏差の意味とは

今までの講座では、分散や標準偏差は、「データのばらけ具合」を表すと説明してきました。
しかし、データが正規分布するという条件においては、「全体のなかでどこらへんにいるか？」の目安となります。

例えば、平均点が65点で標準偏差が10の場合においては、55点～75点の間にあれば68.3%なので、普通の成績だという事が分かります。

逆に「平均-標準偏差×3」の35点以下になると、$100-99.7=0.3$で、さらに下側確率なので半分の0.15%となってしまいます。

 

このように、正規分布の場合は平均と標準偏差を知る事で、データの位置関係が分かる様になるのです。

 

チェビシェフの不等式

確率変数$X$が平均$μ$、標準偏差$\sigma$の正規分布にしたがうとき、「平均±標準偏差×2」の範囲に全体のデータの約95.4%が収まるという話しはしました。

$μ-2\sigma \leqq X \leqq μ+2\sigma$  <-この範囲に95.4%が入ります。

 

これは正規分布に従うという条件があって成り立つ物でした。
しかし、そうでない場合でも下記の事が言えます。

 

なぜこのような事が言えるかというと、どのような分布であっても以下の不等式が成り立つからです。

 

たとえば、$k=2$の場合を考えてみましょう。
$μ-2\sigma \leqq X \leqq μ+2\sigma$を満たさない確率は以下の式で求められます。

$\frac{1}{2^2}=\frac{1}{4}=0.25$

この様に、0.25以下になるので、$μ-2\sigma \leqq X \leqq μ+2\sigma$の範囲内には$1-0.25=0.75$、つまり75%以上が収まるのです。

 

 

ちなみに絶対値記号を使って、以下の式で表す事ができます。

この不等式をチェビシェフの不等式と言います。

 

 

WorStorysetk illustrations by