この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 母比率の推定ってどうやるの?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回はカイ二乗分布について解説します。
カイ二乗分布は母分散の推定をするのに必要ですのでしっかりと押さえていきましょう。
カイ2乗分布とは何か?
カイ2乗分布は、独立に標準正規分布に従う確率変数$X_1、X_2、…、Xn$の2乗和の分布です。
簡単に言うと、確率変数をn個2乗し、それらを合計したものの分布です。
カイ2乗分布は、母集団の分散が既知の時に正規分布する母集団について、そこから抽出した標本の分散がどのような分布を示すかを表す分布です。
他にも独立性の検定や正規性の検定などに使われます。
たとえば、以下の場合を考えてください。
標準正規分布$N(0, 1^2)$にしたがう母集団から、データを無作為に3個選び、二乗してから和を求めます。
これを1000回繰り返し、結果をプロットしなさい。
例えば、一回目の抽出結果が[2, 3, 6]であった場合、
$X = 2^2+3^2+6^2=49$
となります。無作為にデータを選んでいるので、もちろん選ぶたびに結果は変わります。
これを1000回繰り返します。
そうすると、以下のグラフができます。
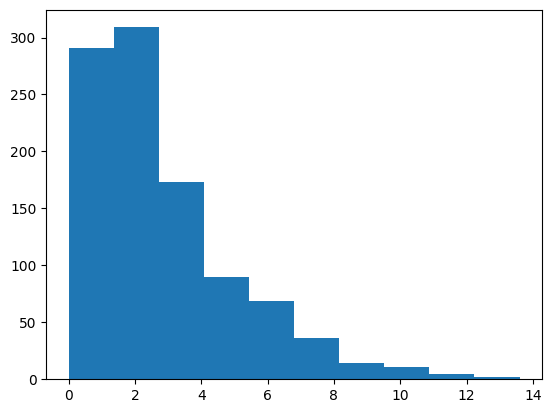
この$X$の分布がカイ2乗分布です。
ちなみにカイは、ギリシャ文字で$\chi$と表現します。
また、今回は3個のデータを抽出しているため、自由度が3です。
自由度とは?
上記の場合では「自由度が3」と言いましたが、これは何を意味しているのでしょうか?
簡単に説明すると、問題分に「データを無作為に3個選び」という記載があります。
これが意味するところは、3個のデータは互いに独立で、自由に値を決められるので、自由度3といいます。
この様に、自由に値を決められるので自由度です。
1個でしたら自由度1ですし、5個でしたら自由度5です。
自由度は$n$で表現される事もありますが、$k$で表される事の方が多いので、本講座では$k$を使います。
自由度ごとの形
自由度1~5の場合のカイ2乗分布の形をまとめたのが↓になります。
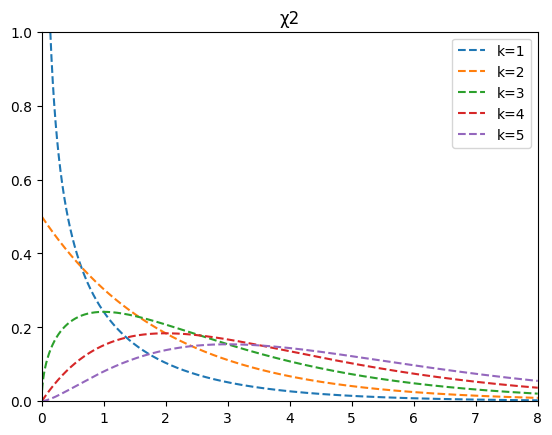
自由度によって形が大きく変わっていますね。
カイ2乗分布の特徴としては以下のものがあります。
- 2乗するので負の値にはならない
- 平均0の標準正規分布から抽出されるので0周辺の値が抽出される確率が高い
- $k$の数が増えるほど山の頂点が右にいく
この様に、カイ2乗分布という言葉は一見すると難しそうに聞こえますが、非常にシンプルで理解しやすいと思います。
確率変数をk個2乗し、それらを合計したものの分布がカイ2乗分布です。
式で表すと↓です。
$X = Z_1^2+Z_2^2…Z_k^2$
この$X$の分布を自由度kのカイ2乗分布といいます。
カイ2乗分布がもつ性質
カイ2乗分布の期待値や分散、またカイ2乗分布がもつ性質を見ていきましょう。
カイ2乗分布の期待値と分散
確率変数$X$が自由度$k$のカイ2乗分布に従っているとき、$X$の期待値$E(X)$と分散$V(X)$は↓になります。
- $E(X)=k$
- $V(X)=2k$
カイ2乗分布の再生性
カイ2乗分布は再生性を持っています。
再生性とは、カイ2乗分布に従う独立な確率変数の和もまたカイ2乗分布に従う性質です。
たとえば、自由度が10であるカイ2乗分布に従う確率変数XとYがあるとします。このとき、X+Yは自由度が20であるカイ2乗分布に従います。
カイ2乗分布に従うデータの95%範囲
前に、正規分布に従うデータの95%範囲について解説したと思います。
その時は、「平均±標準偏差×1.96」の範囲内にデータの95%が収まるという話しをしました。
下の図の青い部分ですね。
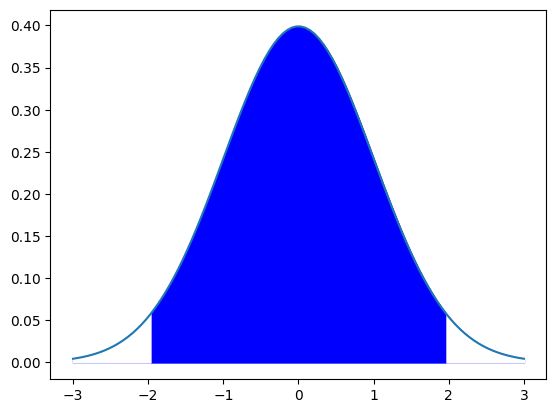
では、カイ2乗分布のばあいはどの様になるかというと、↓の図の白い部分の面積にデータの95%がおさまっています。
ちなみにこれは自由度$k=3$の分布です。
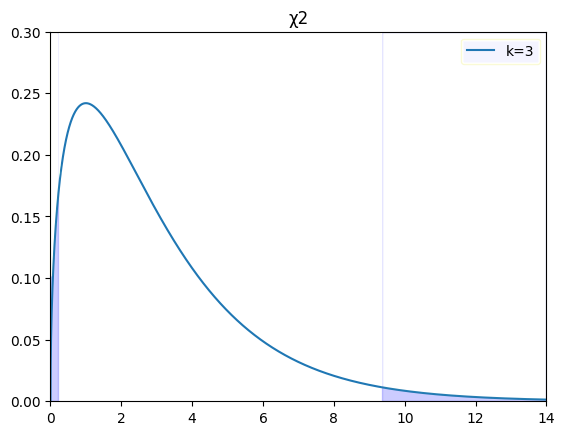
逆に↑の図の青い部分は、下側0.025で上側0.025となっています。
正規分布の際にはこれらのパーセント点を求める際に、標準正規分布表から対応する値を見つけていたと思います。
カイ2乗分布でも同じ様に、表がありますのでそちらから算出します。
カイ2乗分布表
| 0.005 | 0.025 | 0.05 | 0.95 | 0.975 | 0.995 | |
| 1 | 0.00 | 0.00 | 0.00 | 3.84 | 5.02 | 7.88 |
| 2 | 0.01 | 0.05 | 0.10 | 5.99 | 7.38 | 10.60 |
| 3 | 0.07 | 0.22 | 0.35 | 7.81 | 9.35 | 12.84 |
| 4 | 0.21 | 0.48 | 0.71 | 9.49 | 11.14 | 14.86 |
| 5 | 0.41 | 0.83 | 1.15 | 11.07 | 12.83 | 16.75 |
| 6 | 0.68 | 1.24 | 1.64 | 12.59 | 14.45 | 18.55 |
| 7 | 0.99 | 1.69 | 2.17 | 14.07 | 16.01 | 20.28 |
| 8 | 1.34 | 2.18 | 2.73 | 15.51 | 17.53 | 21.95 |
| 9 | 1.73 | 2.70 | 3.33 | 16.92 | 19.02 | 23.59 |
| 10 | 2.16 | 3.25 | 3.94 | 18.31 | 20.48 | 25.19 |
表の見方としては、標準正規分布表と若干違い、赤字の行の部分が自由度になっています。
ですのでまず自由度を確認し、対応する列と交差する値をみます。
例えば、「自由度が2の95%範囲を知りたい」場合を考えましょう。
95%の両側なので、0.025と0.975の範囲内のことですね。
カイ2乗分布表の自由度2の所を見ると、
| 0.005 | 0.025 | 0.05 | 0.95 | 0.975 | 0.995 | |
| 1 | 0.00 | 0.00 | 0.00 | 3.84 | 5.02 | 7.88 |
| 2 | 0.01 | 0.05 | 0.10 | 5.99 | 7.38 | 10.60 |
行が2で、列が0.025と0.975の交差するところが「0.05」と「7.38」という事が分かりました。
ですので、カイ2乗分布の自由度2の場合の95%範囲は、↓になります。
$0.05 \leqq X \leqq 7.38$
まとめ
初めてカイ2乗という言葉を聞いた人にとっては、一回ではなかなか理解しにくい内容だったかもしれません。
大事なポイントとしては、以下の部分ですのでしっかりと覚えておきましょう。
- 正規分布以外にもカイ2乗分布というものがある
- カイ2乗分布は確率変数をk個2乗し、それらを合計したものの分布
- 自由度によって形が変わる
- パーセント点はカイ2乗分布表を使ってもとめる
Work illustrations by Storyset