この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 母平均の仮説検定はどうやるの?
- 片側・両側検定って何?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回の講座は、前回に引き続き母平均の仮説検定についてです。
重要な概念として、片側・両側検定が出てきますので、その点もしっかりと押さえていきましょう。
母分散既知の母平均の仮説検定
前に母平均の推定はやりましたね!
母分散が分かっている場合と分からない場合で少しやり方が違っていたと思います。
母平均の仮説検定も同じで、母分散が分かっている場合と分からない場合とでは求め方が異なります。
この章では、母分散が分かっている場合の仮説検定のやり方を見ていきましょう。
仮説検定の手順
まず、どのように仮説検定を行うのか?その流れを押さえておきましょう。
- 帰無仮説$H_0$と、対立仮説$H_1$を立てる
- 検定統計量を求める
- 棄却域の設定
- 帰無仮説が正しいか検証
この流れにそって検定を行います。
まずは以下の例題を解きながら、その流れを見ていきましょう。
あるパン屋さんで作っているメロンパンは、重量の平均が160gで分散が25であると公表している。
A君がこのメロンパンを5個買ったとき、それぞれの重量は、
[162g, 155g, 153g, 150g, 160g]
であり、A君は公表している数値よりも少し小さいのではないかと感じた。
このメロンパンの母平均160gが正しいのかどうかを、有意水準5%で検定しなさい。
①帰無仮説と対立仮説を立てる
まずは帰無仮説と対立仮説を立てます。
どっちがどっちか混同しやすいですが、帰無仮説が本来棄却を狙う仮説で、対立仮説が主張したい仮説です。
今回の場合ですと、「A君が本当は160gではないのではないか?」と疑っている事から、
- 帰無仮説:母平均は160gである
- $H_0:μ=160$
- 対立仮説:母平均は160gより小さい
- $H_1:μ < 160$
となります。
②検定統計量を求める
続いて検定統計量を求めます。
そのためには標本平均が必要ですので、先に求めます。
標本平均$\bar{X}$を求める
$\bar{X}=\frac{162+155+153+150+160}{5}=156$
$\bar{X}$は正規分布$N(μ, \frac{\sigma^2}{n})$に従います。
検定統計量$Z$を求める
以下の式から検定統計量$Z$を求めます。
$Z=\frac{\bar{X}-μ}{\sqrt{\frac{\sigma^2}{n}}}$
代入して計算します。
$Z=\frac{156-160}{\sqrt{\frac{25}{5}}}=\frac{-4}{\frac{5}{\sqrt{5}}}\fallingdotseq-1.79$
$Z$の値が$-1.79$という事が分かりましたね!
③棄却域を設定する
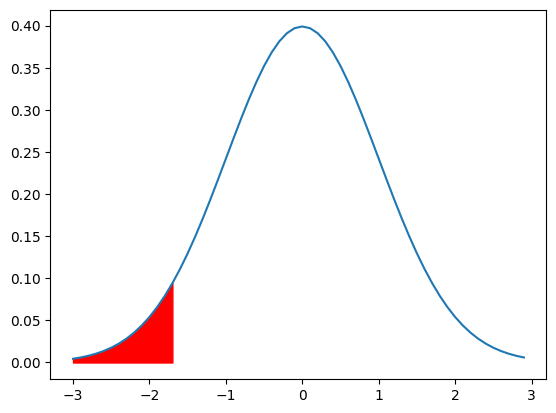
確率変数$Z$は標準正規分布$N(0, 1^2)$に従います。
上の図は、平均0、標準偏差1の標準正規分布をプロットしたものです。
左端の赤い部分が、有意水準を5%に設定した場合の棄却域になります。
つまり、上で求めた検定統計量$Z$がこの赤い部分に入っていると、帰無仮説が棄却されるのです。
棄却域に入っているかの確認はどうやってするのか?
この点が気になりますよね?
上で求めた$-1.79$という検定統計量が棄却域に入っているかどうかが重要ですからね!
どのように求めるかと言うと、
- 有意水準は5%
- なので棄却域は0.05になる
- 標準正規分布表で下側確率が5%となるなる%点が境界値
この様にして、棄却域に入る境界値を求める事ができます。
この境界値が分かれば、棄却域を設定でき、棄却域に入るかどうかの確認が出来ます。
では、標準正規分布表を見てみましょう。
$0.5-0.05=0.45$になる値を探します。
| 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | |
| 1.6 | – | – | – | – | 0.4495 | 0.4505 |
すると、「1.64」と「1.65」がもっとも近い値となり、差も絶対値で0.0005差なので同じです。
ですので、今回の講座では「1.64」を境界値とします。
ちなみに正規分布は左右対象で、今回は下側検定ですので「-1.64」が境界値です。
④帰無仮説が正しいか検証
得られた情報をもとに、帰無仮説が正しいか検証していきましょう。
- 境界値:-1.64
- 検定統計量:-1.79
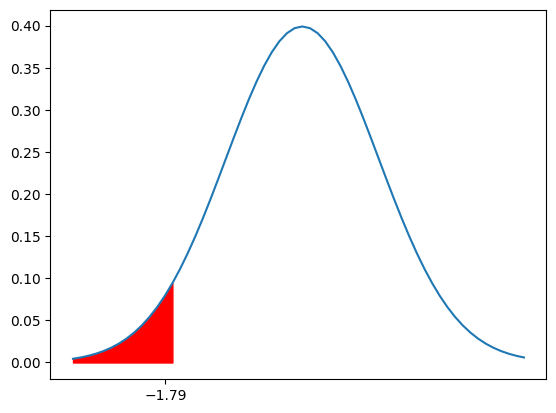
↑の図からも分かる通り、-1.79は棄却域に入っています。
よって、帰無仮説$H_0$は棄却され、対立仮説の「母平均は160gより小さい」が採択されます。
片側・両側検定とは?
上記の例題では、「下側~」という説明が何度か出てきましたが、これがどういった意味なのか?詳しい説明をしていませんでしたね。
検定を行う上で重要な概念ですので、しっかりと覚えておきましょう。
3種類の検定方法
検定を行うときに、どのように検定を行うのか?
大きくわけると以下の3つがあります。
- 母平均$μ$gが$a$より大きいかを検定
- 母平均$μ$gが$a$より小さいかを検定
- 母平均$μ$gが$a$ではないかを検定
前セクションの例題では、「母平均が160より小さいか?」を検定しましたね。
それぞれを詳しく見ていきましょう!
母平均$μ$が$a$より大きいかを検定
下の図のように、母平均より大きいかを検定する場合のことを片側検定(右片側検定)や上側検定と言います。(赤い部分が有意水準5%の棄却域です。)
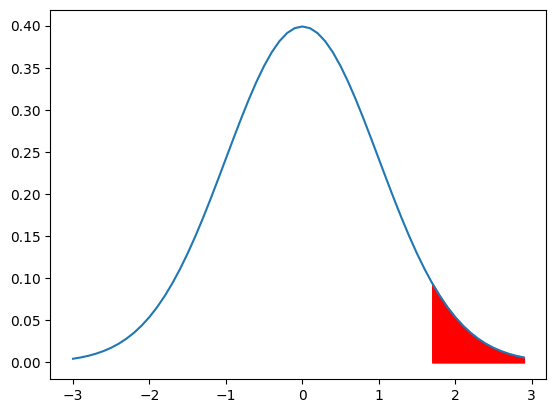
帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:$μ=a$
- 対立仮説:$μ \leqq a$
母平均$μ$が$a$より小さいかを検定
下の図のように、母平均より小さいかを検定する場合のことを片側検定(左片側検定)や下側検定と言います。

- 帰無仮説:$μ=a$
- 対立仮説:$μ \geqq a$
母平均$μ$gが$a$ではないかを検定
下の図のように、母平均が$a$ではない事を検定する場合のことを両側検定と言います。
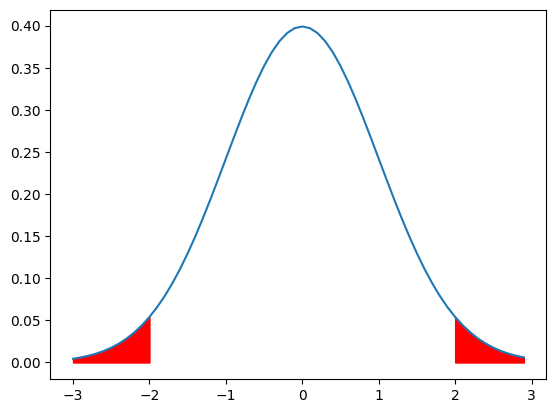
棄却域が両側にあるので両側検定です。
- 帰無仮説:$μ=a$
- 対立仮説:$μ \neq a$
片側検定と両側検定の違い
例えば、有意水準を5%とした場合、棄却域の面積は全体の0.05になります。
片側検定の場合は、その境界値が上側で「1.64」、下側で「-1.64」になることは前のセクションでやりました。
では両側検定の場合も、↓の図のように上側「1.64」、下側「-1.64」で良いのかと言うと違います。
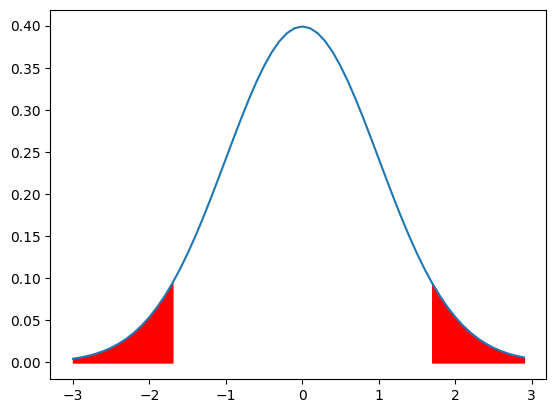
このように、$0.05+0.05=0.1$の面積になってしまいます。
ですので、両側検定の場合の棄却域は$0.025+0.025=0.05$としないといけません。
そのため、両側検定の場合の境界値は標準正規分布表から、$0.5-0.025=0.475$に対応する値です。
それが、「1.96」と「-1.96」なのです。
このように、片側検定と両側検定では境界値が違います。
両側検定の方が、片側に絞ってみたら棄却域が半分になっている点を考慮する事が大切です。
母分散が分からない場合の母平均の仮説検定
当たり前ですが、母平均の仮説検定を行うのに母分散が分からない場合の方が多いです。
母分散が分かっている場合と、分からない場合では若干ですが求め方が変わります。
簡単に説明すると以下の点が違います。
- 検定統計量を求めるのに不偏分散$U^2$を使う
- 標準正規分布では無く、$n-1$の$t$分布に従う
t分布を覚えていますでしょうか?
母平均の推定でやりましたね。
いまいち覚えていない方はコチラの講座から復習しましょう!
母平均の仮説検定のやり方
基本的には母分散既知の場合と変わりません。
- 帰無仮説$H_0$と、対立仮説$H_1$を立てる
- 不偏分散を求める
- 検定統計量を求める
- 棄却域の設定(t分布)
- 帰無仮説が正しいか検証
例題
では実際に例題を基に解き方を見ていきましょう。
あるたこ焼き屋さんでは、タコの大きさを売りにしており、重量30gと銘打って販売していた。
無作為に10個えらび、タコの重量を測ったところ、標本平均は27gで標本標準偏差は3gであったため、本当は30gも無いのではないかと疑惑が沸いた。
このたこ焼き屋のタコは本当に30gあるのかどうかを有意水準5%で検定せよ。
帰無仮説と対立仮説を立てる
問題文から、公表している30g(母平均)よりも小さいのかどうかという所に焦点があります。
そのため、片側検定になるので帰無仮説と対立仮説は以下の通りです。
- 帰無仮説:$μ=30$
- 対立仮説:$μ < 30$
不偏分散を求める
今回は母分散が分からないのでした。
そんな時は母分散の代わりに不偏分散を使うのですが、問題文にあるのは標本の標準偏差です。
ですので、標準偏差を不偏分散にする必要があります。
どうやるのかというと、非常にシンプルです。
$U^2=S^2\frac{n}{n-1}$
この計算をすれば良いだけです。
まず$S^2$は標本分散であり、問題文で与えられているのは標本標準偏差ですので、標本分散を求めます。
ただ二乗すれば良いだけです。
$S^2=3^2=9$
$S^2$が9と分かりました。
また$n$は問題文から10という事が分かっているので、これで不偏分散$U^2$を求められます。
$U^2=9×\frac{10}{10-1}=\frac{90}{9}=10$
これで不偏分散$U^2$が10だという事が分かりました。
検定統計量を求める
不偏分散を使って検定統計量を求めるには以下の式に代入します。
$T=\frac{\bar{X}-μ}{\sqrt{\frac{U^2}{n}}}$
また今までの情報を整理すると、
- $\bar{X}=27$
- $μ=30$
- $n=10$
- $U^2=10$
ですので、代入していきましょう。
$T=\frac{27-30}{\sqrt{\frac{10}{10}}}=\frac{-3}{\sqrt{1}}=-3$
検定統計量が$-3$という事が分かりましたね!
棄却域の設定(t分布)
統計量$T$は自由度$n-1$のt分布に従います。
今回は$n=10$ですので、自由度9です。
また、有意水準は5%なので0.05です。
t分布表からこれに対応する値を探します。
| 0.005 | 0.01 | 0.025 | 0.05 | |
| 9 | 3.250 | 2.821 | 2.262 | 1.833 |
「1.833」だという事が分かりました。
しかし、今回は下側検定を行いたかったのでした。
そこで、t分布は左右対象という性質を利用し、プラスマイナスを逆にして「-1.83」が%点だという事が分かりました。
帰無仮説が正しいか検証
- 検定統計量:$-3$
- 境界値:$-1.83$
この結果から、検定統計量が棄却域に含まれる事が分かりました。
帰無仮説が棄却され、対立仮説である「$μ<30$」が採択されました。
このようにして、母分散が分からない場合の母平均の検定を行います。
流れを覚えてしまえば、あとは機械的に解いていけば良いので、この一連の流れを覚える事が大切です。