F分布で等分散の検定！【0から始める統計検定2級講座㉜】

この講座の対象者は以下の方を想定しています。

数学は中学レベルしか分からないけど統計検定2級に合格したい
どの参考書を見ても数式だらけで理解できない
F分布ってなに？
F分布はどんな時に使うの？

この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。

今回は、正規分布から派生したF分布についてです。
正規分布、カイ2乗分布、t分布と習ってきましたが、ついにF分布の登場です。

今までの内容が分かっていれば、すんなり理解できると思います。

Contents

F分布とは？
- F分布の形
等分散の検定方法
練習問題
- 練習問題①

F分布とは？

F分布がどのようなものかというと、自由度$f_1$のカイ2乗分布に従う確率変数を$X$、自由度$f_2$のカイ2乗分布にしたがう確率変数を$Y$とします。
$X$と$Y$が独立であるとき、↓が従う分布のことを、自由度$(f_1, f_2)$のF分布というのです。

$F=\frac{\frac{X}{f_1}}{\frac{Y}{f_2}}$

えいせい

これだけだと何のことか意味が分からないと思いますので、分布の形を見てみましょう。

F分布の形

まず、以下の3つの自由度のセットを用意します。

(3, 8)
(7, 5)
(10, 10)

この自由度をもとにプロットしたのが↓になります。

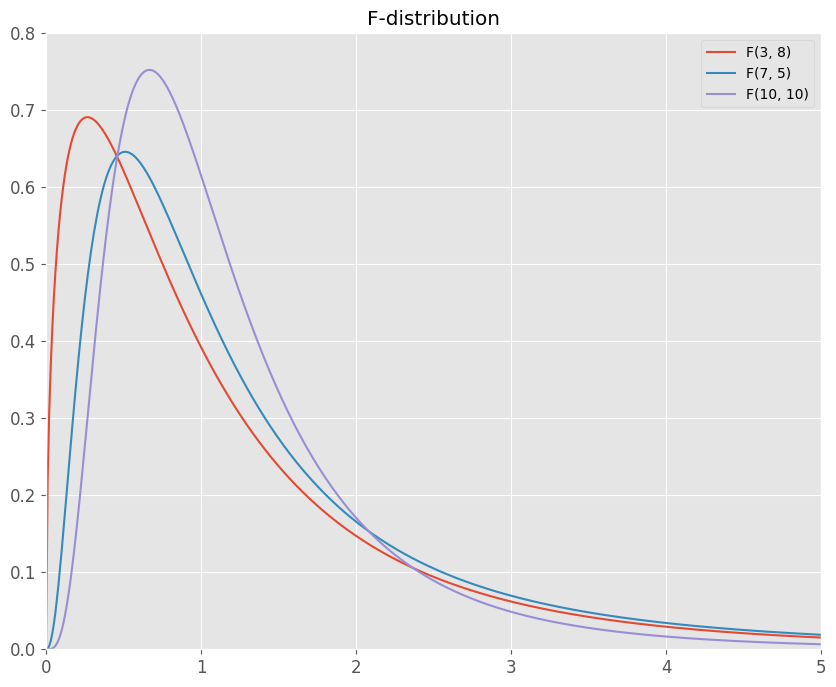
このように、F分布は2つの自由度によって形が変わります。
この自由度が2つというのが重要なポイントです。

また、見てわかる様に左右非対称な山形の分布です。

等分散の検定方法

等分散の検定方法とはどういう事かというと、2つの母集団の分散がが等しいかどうかを検定するということです。

この検定に使うのがF分布なのです。

等分散の検定の流れ

等分散の検定の流れは、今までの検定の流れと同じです。

帰無仮説と対立仮説を立てる
検定統計量を求める
棄却域を設定
帰無仮説が正しいか検証

この順番で解いていきます。

例題

ではさっそく例題をもとに解き方を見ていきましょう。

あるケーキ屋さんでは、メロンを$X$農家と$Y$農家から仕入れている。
$X$農家のメロンを6個選んで重さを測ったところ、不偏分散は64であった。
$Y$農家のメロンを8個選んで重さを測ったところ、不偏分散は49であった。
この2つの農家のメロンの重さの母分散に差があるといえるか？有意水準5%で検定しなさい。

①帰無仮説と対立仮説

ではいつも通り帰無仮説と対立仮説を立てていきましょう！
$X$農家と$Y$農家の母分散は、それぞれ$\sigma_X^2$、$\sigma_Y^2$とします。

まず今回の検定は等分散かの検定なので、両側検定になり↓のようになります。

帰無仮説：$\sigma_X^2=\sigma_Y^2$
対立仮説：$\sigma_X^2 \neq \sigma_Y^2$

②検定統計量を求める

F分布の検定統計量$F$はどのように求めるかというと、以下の式から求める事ができます。

$F=\frac{U_X^2}{U_Y^2}$

ちなにみ$U^2$は不偏分散を表しています。
母分散とは違いますので注意しましょう！

不偏分散は問題文に書いてありますね。

$U_X^2=64$
$U_Y^2=49$

ですので、この値を式に代入します。

$F=\frac{64}{49}=1.306$…検定統計量

このようにして、検定統計量$F$が$1.306$という事が分かりました。

棄却域の設定

まず、検定統計量$F$は、自由度$(m-1、n-1)$のF分布にしたがいます。
$m$は$X$農家の自由度で、$n$はY農家の自由度です。

ですので、今回の自由度は$(5, 7)$という事になります。

自由度$(5, 7)$の分布は以下のようになり、赤い部分が左右2.5%の棄却域です。

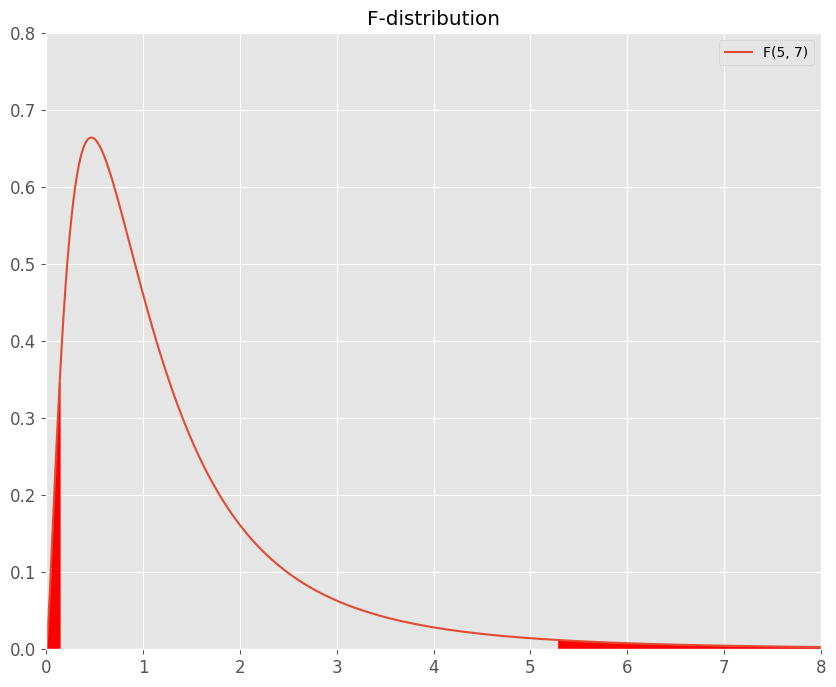
つづいて検定統計量が棄却域に入るかを確認するために境界値を求めていきます。
いつも通りこれの算出にはF分布表を使って求めるのですが、F分布表は今までのものと若干見方が異なります。

↓がF分布表ですが、行と列はそれぞれ自由度の値になります。
行(→)が$m$の自由度で、列(↓)が$n$の自由度になります。

	1	2	3	4	5	6	7	8	9	10
1	647.789	799.500	864.163	899.583	921.848	937.111	948.217	956.656	963.285	968.627
2	38.506	39.000	39.165	39.248	39.298	39.331	39.355	39.373	39.387	39.398
3	17.443	16.044	15.439	15.101	14.885	14.735	14.624	14.540	14.473	14.419
4	12.218	10.649	9.979	9.605	9.364	9.197	9.074	8.980	8.905	8.844
5	10.007	8.434	7.764	7.388	7.146	6.978	6.853	6.757	6.681	6.619
6	8.813	7.260	6.599	6.227	5.988	5.820	5.695	5.600	5.523	5.461
7	8.073	6.542	5.890	5.523	5.285	5.119	4.995	4.899	4.823	4.761
8	7.571	6.059	5.416	5.053	4.817	4.652	4.529	4.433	4.357	4.295
9	7.209	5.715	5.078	4.718	4.484	4.320	4.197	4.102	4.026	3.964
10	6.937	5.456	4.826	4.468	4.236	4.072	3.950	3.855	3.779	3.717

今回は$m$(行)が$5$で、$n$(列)が$7$に対応する値をさがします。
すると、$5.285$という事が分かりました。
これは上側の境界値です。

では続いて下側の境界値も求めたいのですが、F分布の場合は求め方が複雑です。
左右非対称なため、単純に求める事ができません。
以下のようにして求めます。

下側の境界値$p$点は、自由度$(n, m)$のF分布にしたがう確率変数の上側$p$点の逆数に等しい

これだけだと何を言っているのか分からないですよね、、
具体的に見ていきましょう。

まず、自由度は$(m, n)$では無く$(n, m)$になるのがポイントです。
ですので、左右逆になり自由度$(7, 5)$になります。

F分布表から行(→)が$7$で、列(↓)が$5$に対応する値を探すと、$6.853$という事が分かります。

これの逆数を求めれば良いのですが、逆数を求めるには1を割れば良いのです。

$\frac{1}{6.853}=0.146$…下側境界値

帰無仮説が正しいか検証

上記の結果をまとめると、

上側境界値$p$点：$5.285$
下側境界値$p$点：$0.146$
検定統計量$F=1.306$

このような結果になりました。

棄却域をプロットすると↓になります。

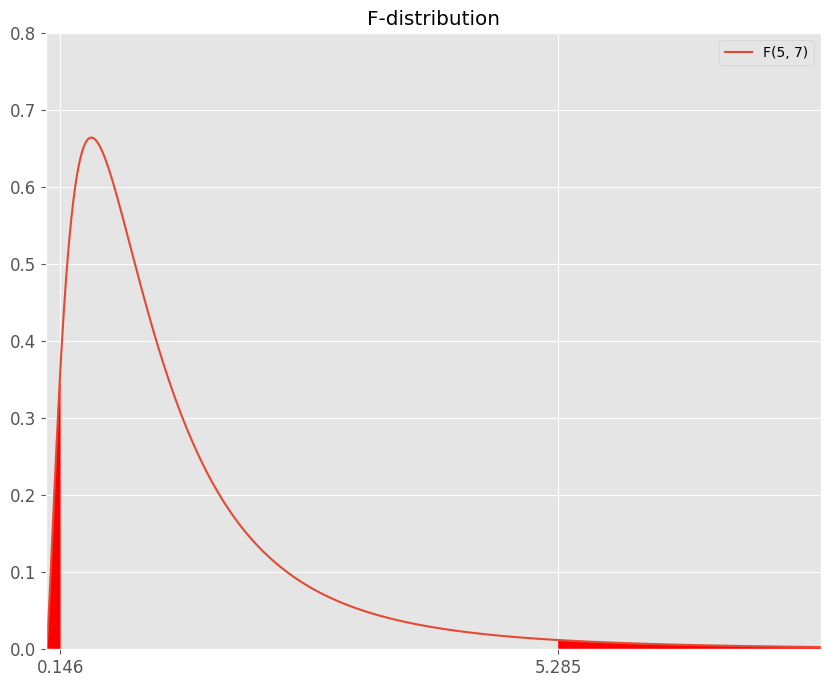
この結果から、検定統計量$F$は棄却域に入らない事が分かりました。
したがって帰無仮説は棄却されません。

$X$農家と$Y$農家の母分散は等しくないとはいえないという結論になりました。

えいせい

F分布は境界値の求め方が若干難しいですが、その他の流れは今までの流れと一緒ですのですぐに覚えられると思います。

練習問題

上記のF分布表を使って次の問題に答えなさい。

練習問題①

パン屋さん$X$と$Y$のあんパンの重量を測ったところ、$X$店では8個測定し、重量の平均は52gで、標本標準偏差は8gであった。いっぽう$Y$店のあんパンは7個測定し、重量平均47gで、標本標準偏差は3gであった。この2つのパン屋の母分散は等しいと言えるか？有意水準5%で検定しなさい。

答え…等しくない

①帰無仮説と対立仮説

まずは以下の様に帰無仮説と対立仮説を立てます。

帰無仮説：$\sigma_X^2=\sigma_Y^2$
対立仮説：$\sigma_X^2 \neq \sigma_Y^2$

②検定統計量を求める

検定統計量を求めるためには不偏分散が必要です。
しかし、問題文には不偏分散の記載はないために、標本標準偏差から求める必要があります。
不偏分散$U^2$は標本分散$S^2$に$\frac{n}{n-1}$を掛ける事で求められます。
また問題文では標本標準偏差が記載してあるので、それを標本分散にする必要があります。