この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 適合度検定ってなに?
- 観測値とか理論値の意味が分からない
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回は、適合度検定について解説します。
少し理解するのが難しい場面もありますが、ひとつずつしっかりと理解していきましょう。
適合度検定とは何か?
適合度検定とは、観測されたデータが特定の分布に従っているかどうかを検定する統計手法です。
適合度検定では、観測されたデータの度数と、特定の分布に従うと仮定した場合の期待度数を比較します。
この二つの度数の差が小さいほど、観測されたデータは特定の分布に従っている可能性が高くなります。
適合度検定が役立つシーン
以下のシーンで使われることが多いです。
- あるデータの分布が知られている分布と一致するかどうかを検定する。
- あるデータの分布が別のデータの分布と一致するかどうかを検定する。
- あるデータの分布が変化したかどうかを検定する。
適合度検定のやり方
適合度検定も今までの検定と同じで、以下の流れに沿って行います。
- 帰無仮説と対立仮説を立てる
- 検定統計量を求める
- 棄却域を設定する
- 帰無仮説が正しいか検証
では実際に例題を基に解き方を見ていきましょう。
例題
A君とB君がじゃんけんを90回したところ、以下の結果となった。
A君はB君よりじゃんけんが強いと言えるか?
有意水準5%で検定せよ
| A君の勝ち | B君の勝ち | あいこ | |
| 回数 | 42 | 22 | 26 |
本来じゃんけんの確率としては、
- A君が勝つ確率
- B君が勝確率
- あいこの確率
上記は全て$\frac{1}{3}$になるはずですが、結果から見るとA君の勝利回数に偏っているように見えます。
統計的に有意な差があるのか、見ていきましょう。
①帰無仮説と対立仮説
まず、帰無仮説と対立仮説を立てます。
- 帰無仮説:A君とB君のじゃんけんの勝率は一緒
- 対立仮説:A君の方がじゃんけんが強い
②検定統計量を求める
適合度検定の検定統計量を求める方法は今までと少し違います。
以下の式から求める事ができます。
$\chi^2=\frac{(実測値_1-理論値_1)^2}{理論値_1}+\frac{(実測値_2-理論値_2)-2}{理論値_2}+…+\frac{(実測値_n-理論値_n)-2}{理論値_n}$
実測値と理論値という新しい単語が出てきましたね!
それぞれの意味としては、
- 実測値:実際に計測された値。今回の場合は実際にA君とB君がじゃんけんした結果
- 理論値:理論的な確率分布にしたがった値。今回の場合はA君が勝つ・B君が勝つ・あいこはそれぞれ$\frac{1}{3}$になる。
クロス集計表にまとめると↓になります。
| A君の勝ち | B君の勝ち | あいこ | 合計 | |
| 回数(実測値) | 42 | 22 | 26 | 90 |
| 確率 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | 1 |
| 理論値 | 30 | 30 | 30 | 90 |
では実際に上記の式に代入して検定統計量$\chi^2$を求めていきましょう。
$\chi^2=\frac{(42-30)^2}{30}+\frac{(22-30)^2}{30}+\frac{(26-30)^2}{30}$
$=4.8+2.133+0.53=7.463$
このようにして、検定統計量$\chi^2=7.463$という事が分かりました。
このように、理論値と実測値のズレを測るのが適合度検定です。
ズレが大きいほど検定統計量の値が大きくなり、ズレが小さいほど0に近づきます。
③棄却域の設定
適合度の検定では$\chi^2$分布を使います。
$\chi^2$分布は以下のように、自由度$k$の数によって形が変わるのでした。
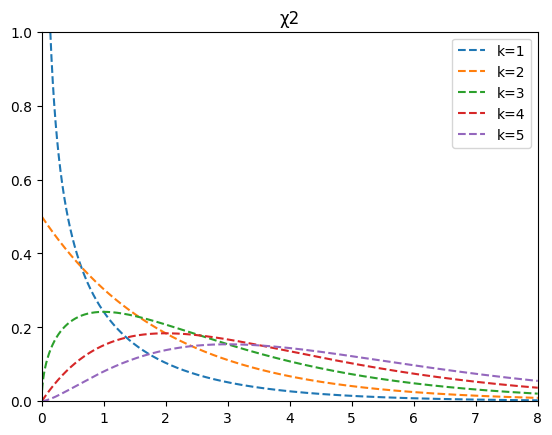
棄却域を設定するうえで、まずは自由度$k$が重要になってきます。
自由度は$k-1$するんでした。
そして、この$k$に入る値は、クロス集計表の列の個数です。
今回は「A君の勝ち」、「B君の勝ち」、「あいこ」の3つですので、$3-1$をして、自由度は$k=2$になります。
今回は有意水準5%の上側検定ですので、$\chi^2$分布表から対応する値を探します。
列は1-0.05=0.95で、行(自由度)は2のところを見ます。
| 0.005 | 0.025 | 0.05 | 0.95 | 0.975 | 0.995 | |
| 1 | 0.00 | 0.00 | 0.00 | 3.84 | 5.02 | 7.88 |
| 2 | 0.01 | 0.05 | 0.10 | 5.99 | 7.38 | 10.60 |
| 3 | 0.07 | 0.22 | 0.35 | 7.81 | 9.35 | 12.84 |
境界値は$5.99$という事が分かりました。
帰無仮説が正しいか検証
結果をまとめると、
- 検定統計量$Z=7.463$
- 境界値:$5.99$
です。
この結果から、棄却域に入る事がわかりましたので、帰無仮説は棄却されます。
A君はB君よりじゃんけんが強いと言える事がわかりました。
適合度検定の求め方まとめ
このように、いつもの検定の流れに沿って行えば、適合度検定も簡単に出来ると思います。
ただ、一番のネックとなる所はクロス集計表を作るところですね。
実測値と理論値の値がどれになるのかを冷静に見極めましょう!
これが分かればサクッと解く事が出来ると思います。
練習問題
では最後に練習問題にチャレンジしましょう。
以下のカイ2乗分布表を使ってください。
カイ2乗分布表
| 0.005 | 0.025 | 0.05 | 0.95 | 0.975 | 0.995 | |
| 1 | 0.00 | 0.00 | 0.00 | 3.84 | 5.02 | 7.88 |
| 2 | 0.01 | 0.05 | 0.10 | 5.99 | 7.38 | 10.60 |
| 3 | 0.07 | 0.22 | 0.35 | 7.81 | 9.35 | 12.84 |
| 4 | 0.21 | 0.48 | 0.71 | 9.49 | 11.14 | 14.86 |
| 5 | 0.41 | 0.83 | 1.15 | 11.07 | 12.83 | 16.75 |
| 6 | 0.68 | 1.24 | 1.64 | 12.59 | 14.45 | 18.55 |
| 7 | 0.99 | 1.69 | 2.17 | 14.07 | 16.01 | 20.28 |
| 8 | 1.34 | 2.18 | 2.73 | 15.51 | 17.53 | 21.95 |
| 9 | 1.73 | 2.70 | 3.33 | 16.92 | 19.02 | 23.59 |
| 10 | 2.16 | 3.25 | 3.94 | 18.31 | 20.48 | 25.19 |
練習問題①
答え:日本人全体の血液型分布と一緒ではないとは言えない
①帰無仮説と対立仮説を立てる
- 帰無仮説:日本人全体の血液型分布と一緒
- 対立仮説:日本人全体の血液型分布と一緒ではない
②検定統計量を求める
まず、クロス集計表にまとめます。
| A型 | B型 | O型 | AB型 | 合計 | |
| 実測値 | 68 | 62 | 38 | 32 | 200 |
| 確率 | 0.3 | 0.3 | 0.25 | 0.15 | 1 |
| 理論値 | 60 | 60 | 50 | 30 | 200 |
次に、公式から検定統計量を求めます。
$\chi^2=\frac{(68-60)^2}{60}+\frac{(62-60)^2}{60}+\frac{(38-50)^2}{50}+\frac{(32-30)^2}{30}$
$=1.0667+0.0667+2.88+0.1333=4.1467$
③棄却域の設定
自由度は血液型のカテゴリー数から1を引くので、$4-1=3$です。
また問題分から両側検定ですので、0.025と0.975に対応する値をさがすと、
境界値は以下の値という事が分かります。
- $0.22$
- $9.35$
④帰無仮説が正しいか検証
上記の結果から、帰無仮説は棄却されませんでした。
日本人全体の血液型分布と一緒ではないとは言えない事が分かりました。
Work illustrations by Storyset














