この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 偏相関係数ってなに?
- 層別解析ってなにするの?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回は、偏相関係数と層別解析について解説します。
相関を学ぶ上でこれらも重要な要素になってくるので、しっかりと学びましょう。
偏相関係数とは?

偏相関係数を簡単に説明すると↓になります。
- 2つの変数の間にある関係の強さを3つ目の変数の影響を取り除いて表したもの
- -1から1までの範囲で表される
- -1に近いほど負の偏相関係数
- 1に近いほど正の偏相関係数
- 0に近いほど偏相関係が無い
偏相関係数の例
例えば、身長と体重の関係を見ると、身長が高い人ほど体重が多い傾向があります。この場合、身長と体重の間には正の相関係数があるのは分かりますね。
しかし、この相関係数は、年齢の影響によって生じている可能性があります。
なぜなら、年齢が高い人ほど身長も体重も多い傾向があるからです。
偏相関係数は、この年齢の影響を取り除いて、身長と体重の関係の強さを表すことができます。
例えば、年齢を調整した偏相関係数は、身長と体重の間には依然として正の相関係数があることがわかります。これは、身長と体重の間には年齢の影響を除いても、相関関係があることを示しています。
偏相関係数は、2つの変数の間にある関係の強さを理解するために非常に有効なツールです。特に、3つ目の変数の影響によって生じていると思われる相関係数を分析する場合に有効です。
偏相関係数の求め方
では実際に例題をもとに偏相関係数の求め方を見ていきましょう。
例題
あるショップの気温の変化と「アイスの売上」、「浮き輪の売上」を表にしたのが↓である。
また、それぞれの相関係数は
- 気温とアイスの売上:$0.967$
- 気温と浮き輪の売上:$0.833$
- アイスの売上と浮き輪の売上:$0.840$
となっている。
このとき、アイスの売上と浮き輪の売上の偏相関係数を求めよ。
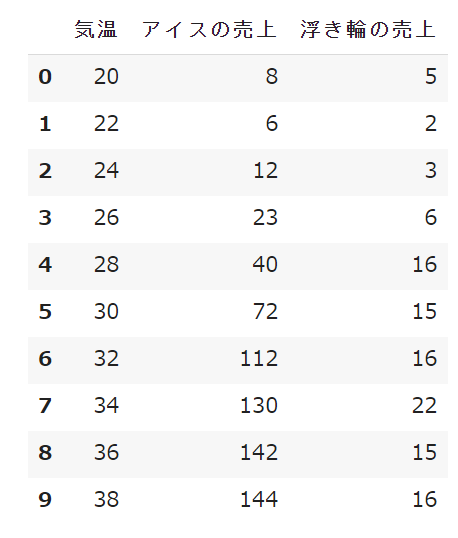
このように、気温の影響をのぞき、アイスの売上と浮き輪の売上にどのような相関があるのかを、偏相関係数を出して見ることができます。
偏相関係数を求める式
では実際にどのように求めれば良いのかというと、以下の式から求める事ができます。
$r_{xy・z}=\frac{r_{xy}-r_{xz}r_{yz}}{\sqrt{1-r_{xz}^2}\sqrt{1-r_{yz}^2}}$
複雑な式ですね。でもやる事はシンプルなので怯む必要はありません。
それぞれの記号の意味をまず整理しましょう。
特に、アイスの売り上げ、浮き輪の売り上げ、気温をそれぞれ$x,y,z$とおくのですが、$z$の影響を除いた偏相関係数$r_{xy・z}$を求めるので、$z$は気温です。
- $x=アイスの売り上げ$
- $y=浮き輪の売り上げ$
- $z=気温$
- $r_{xy・z}=偏相関係数$
- $r_{xy}=xとyの相関係数(アイスと浮き輪)$
- $r_{xz}=xとzの相関係数(アイスと気温)$
- $r_{yz}=yとzの相関係数(浮き輪と気温)$
また、問題文から$r_{xy}=0.840$、$r_{xz}=0.967$、$r_{yz}=0.833$ということが分かっていますので、これらを式に代入してみましょう。
$r_{xy・z}=\frac{0.840-0.967×0.833}{\sqrt{1-0.967^2}\sqrt{1-0.833^2}}=\frac{0.034}{0.141}=0.241$
このようにして、アイスの売り上げと浮き輪の売り上げの偏相関係数は$0.241$ということが分かりました。
この2つの相関はあまりないことが分かりましたね!
層別解析
続いて、層別解析について解説します。
層別解析とは、大きなグループをいくつかの小さな「層」に分けて、それぞれの層ごとに統計的な解析を行う方法です。これにより、全体のグループに潜むばらつきや傾向をより詳細に把握することができます。
層別解析の例
例えば、全体の人口を男性と女性に分けて、それぞれの性別ごとに身体測定をする場合を考えてみましょう。
層別解析では、まず男性と女性の2つの層に分けて、それぞれの身長と体重を測ります。
これによって、性別ごとに異なる傾向や関連性が明らかになりますね。
層別解析のメリット
層別解析の利点は、全体の平均だけでは見逃してしまうような細かい傾向や差異を捉えることができることです。
大きなグループを細かい部分に分けて、それぞれの部分で起こっていることを調べる方法だと言えます。
身長と体重を層別解析してみよう
例えば、男女各10人ずつの身長と体重を散布図のプロットした図が↓です。
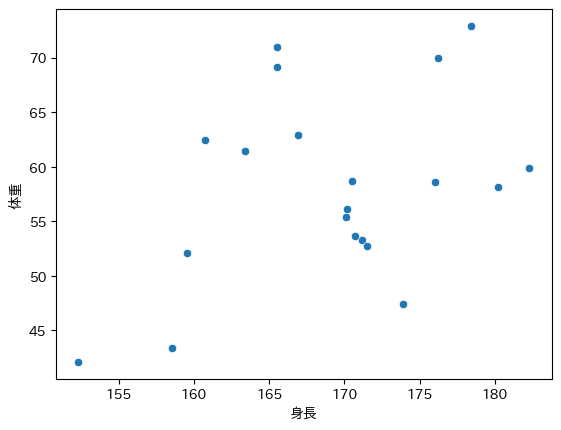
散らばってはいますが、右上がりになっているので、身長と体重には正の相関があるのはパッと見で分かりますね。
しかし、これだと男女ごとの層別に見ることができません。
ですので、男と女で色を分けてプロットしたのが↓です。
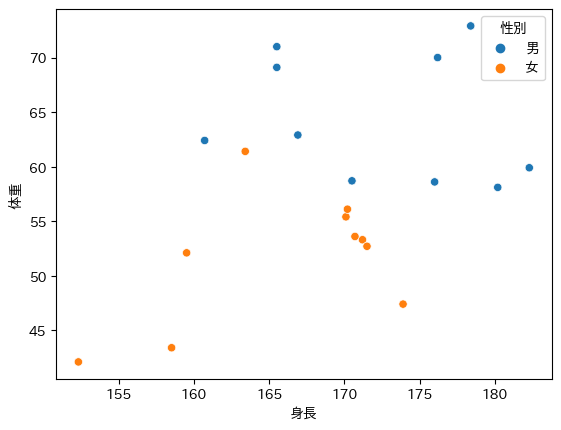
男は青、女はオレンジの点でプロットしています。
このようにすると、それぞれの層でどのようなデータをしているのかが、より鮮明に見ることができます。
男女別にした身長と体重の平均と、全体の平均を比べると以下のようになります。
| 身長 | 体重 | |
| 男 | 172.22 | 64.36 |
| 女 | 166.13 | 51.75 |
| 合算 | 169.17 | 58.05 |
相関係数の練習問題
①
答え:$0.095$
$r_{xy・z}=\frac{0.83-0.86×0.93}{\sqrt{1-0.86^2}\sqrt{1-0.93^2}}=\frac{0.0302}{0.31648}=0.095$
Work illustrations by Storyset














