この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 単回帰分析ってなに?
- 最小二乗法はどうやって計算するの?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回は、単回帰分析と最小二乗法について解説します。
回帰分析は機械学習の入口みたいなものですので、統計検定2級に受かりたい方だけでなく、将来データサイエンティストを目指している方にとっても非常に重要な内容です。
回帰分析とはなにか?
回帰分析とは、ある変数(目的変数)が他の変数(説明変数)によってどのように説明されるかを統計的に分析する手法です。
回帰分析の目的は、説明変数と目的変数の関係を明らかにし、目的変数の値を説明変数から予測することのできる回帰式を求めます。
目的変数と説明変数とは?
回帰分析を理解するうえで、重要な用語として目的変数と説明変数があります。
例えば、以下のケースで考えてみましょう。
マンションAの適正な「販売価格」を予想したい。
そのために、5件分の「駅からの距離」、「築年数」、「販売価格」のデータをまとめたのが以下の表である。
| 駅からの距離 | 築年数 | 販売価格 | |
| マンションA | 5分 | 5年 | ? |
| マンション① | 12分 | 20年 | 2500万円 |
| マンション② | 3分 | 12年 | 3200万円 |
| マンション③ | 7分 | 15年 | 3000万円 |
| マンション④ | 15分 | 8年 | 2800万円 |
| マンション⑤ | 3分 | 14年 | 3300万円 |
このように、与えられた情報からマンションAの販売価格を予測するのに使うのが回帰分析です。
この場合、目的変数と説明変数は↓になります。
- 目的変数(被説明変数):「販売価格」
- 説明変数:「駅からの距離」・「築年数」
目的変数が予測したい変数のことで、説明変数は因果関係における原因の変数です。
ちなみに目的変数は教材によっては被説明変数と言われますが、同じものを指しています。
回帰式とは?
回帰分析の肝は回帰式を求めることです。
回帰式が分かれば、様々なデータを予測することができるようになります。
回帰式は↓の形のものです。
$y=β_0+β_1x$
それぞれの記号の意味としては、
- $y=目的変数$
- $β_0=切片$
- $β_1=傾き$
- $x=説明変数$
となっています。
例えば、$β_0=12$、$β_1=3$のときに、説明変数$x$が5の場合の目的変数$y$を求めるとします。
回帰式から、
$y=12+3×5=27$
目的変数$y=27$ということが求められます。
同じようにして、説明変数$x$の値を4や7にしても、目的変数$y$の値を求めることができますね。
上記の式から、傾きである$β_1$が1増えると、3ずつ増えるのが回帰式から見て取れますね。
このように、回帰式が分かれば、上記例の「駅からの距離」「築年数」の値から、販売価格(目的変数$y$)を求めることが出来るのです。
回帰直線
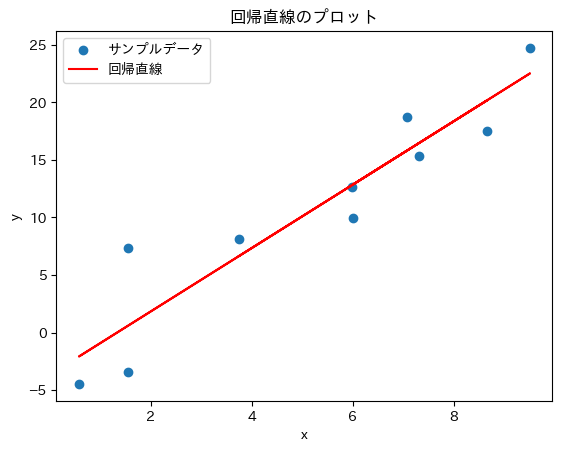
赤い直線のことを回帰直線と言います。
この直線を良い感じにプロットすることが回帰分析で重要です。
詳しくは後述します。
ちなみに回帰直線の正体は回帰式です。
$y=β_0+β_1x$の$x$に値を連続で代入していくと、$y$の値も連続で出てきますよね?
その点をつなげていき、線になったのが回帰線直線です。
回帰分析の種類
回帰分析を大きく2つに分けると以下の2つに分けられます。
- 単回帰分析
- 重回帰分析
それぞれの違いとしては、説明変数が1つだけの場合は単回帰分析です。
上記の例のように、説明変数が「駅からの距離」「築年数」など、複数になってしまう場合においては重回帰分析と言います。
回帰直線の求め方
では、回帰直線についてもう少し深堀りしていきましょう。
さきほど、良い感じの直線を引くことが大事だと説明しましたが、それがどういう事かと言うと、
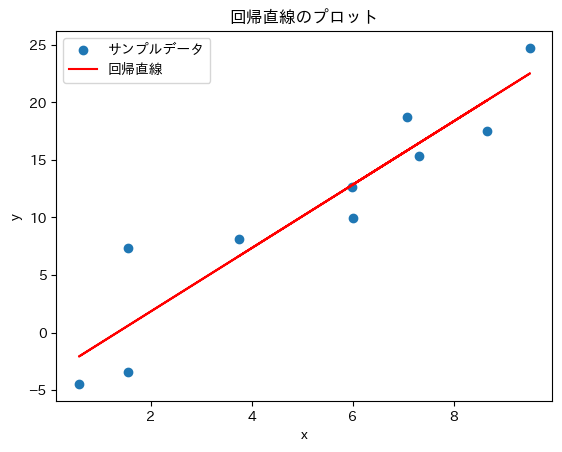
このように、良い感じにすべての点の中心を通っているような線が理想です。
逆に↓のように、偏ってしまっている線はよくありません。
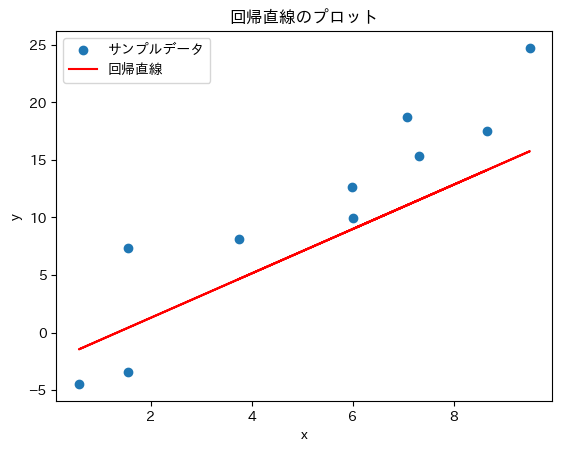
最小2乗法で回帰直線を求める
ではどうやって回帰直線をもとめるかというと、ズレを一番小さくする直線を求めます。
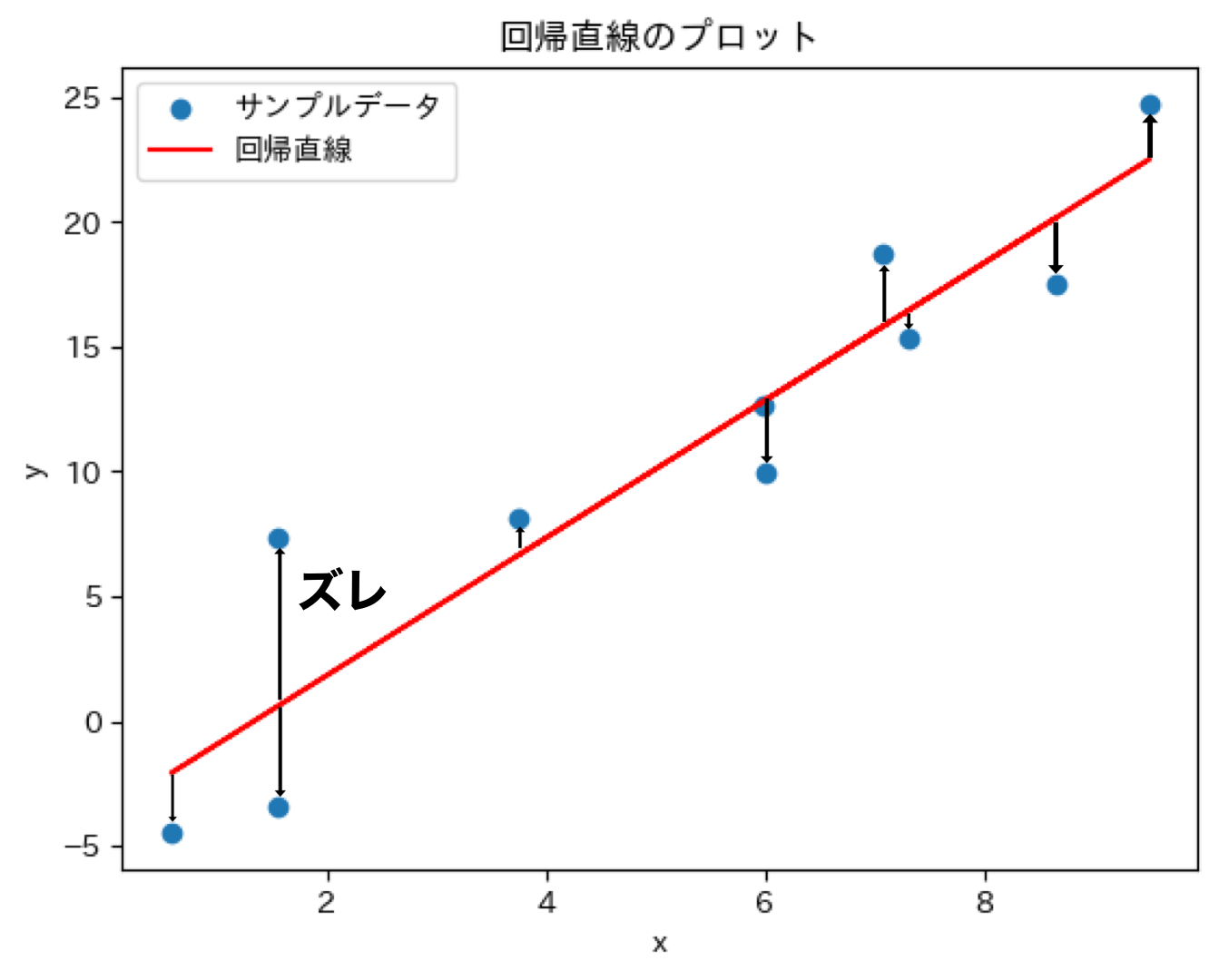
ズレが何かというと、回帰直線から各値までの距離のことです。
このズレの総和を一番小さくすることが重要です。
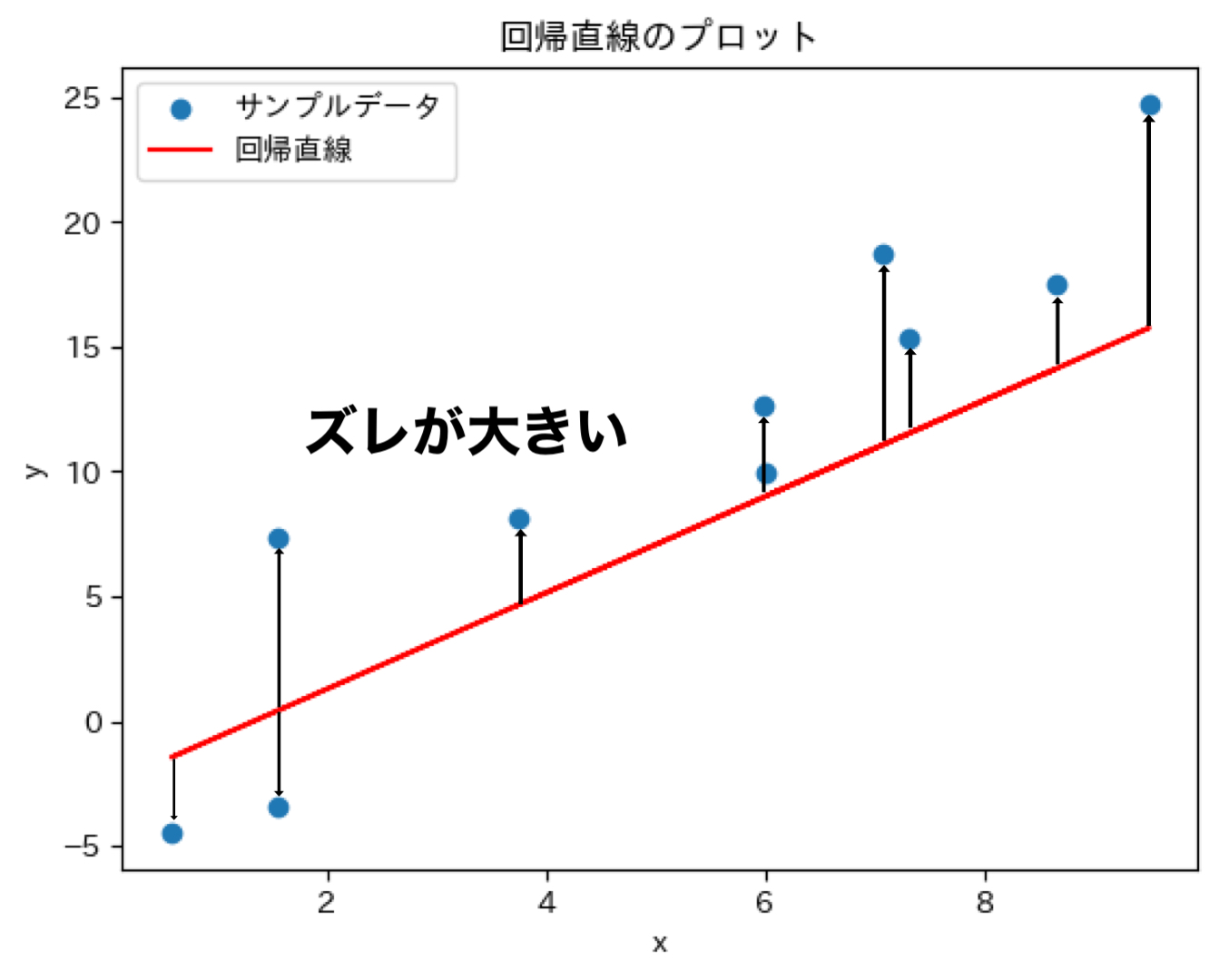
例えば、↓のような回帰直線を引いてしまうと、ズレが大きくなってしまい、ズレの総和が増えてしまいます。
ちなみにズレは目的変数の$y$軸のみで、$x$軸では発生しません。
では、このズレをどうやって計算するかというと、例えば一個目の点を$(x_i,y_i)$とおきます。
そうすると、回帰直線上の座標は回帰式から$y=β_0+β_1x_i$になります。(単純に回帰式の$x$に$x_i$を代入しただけです。)
このように考えると、データの座標(上の図の青い点)と、同じ$x$軸上の回帰直線の座標が分かるので、↓のように引くことでズレが求まります。
$y_i-(β_0+β_1x_i)$
これを計算することで、ひとつの値でのズレの量が求まります。
しかし、このままだとプラスもマイナスの値もあるので、2乗が必要です。
また、総和もしますので、↓の式になります。
$\sum_{n=1}^{n}\{y_i-(β_0+β_1x_i)\}^2$
この式の結果が最小になるように、$β_0(切片)$と$β_1(傾き)$を求めることが重要です。
このことを最小2乗法と言います。
回帰直線が必ず通る点
覚えておいて欲しい点として、$β_0$と$β_1$は以下の式で求めることができます。
- $β_0=\frac{S_xy}{S_x^2}=r_{xy}\frac{S_y}{S_x}$
- $β_1=\bar{y}-b\bar{x}$
この時重要なのが、$β_1$の式から回帰直線は$(\bar{x}, \bar{y})$を通るという事です。
決定係数とは?
もうひとつ覚えておいて欲しいものとして決定係数があります。
これは
決定係数=回帰直線の説明力の指標
のことです。
ようは、回帰直線がデータをどれくらい説明できるのか?の数値だと思って頂ければ大丈夫です。
細かい導入しきは省きますが、決定係数は$R^2$であらわされ、以下の式で求めることができます。
$R^2=r_{xy}^2$
ようは、相関係数の2乗が決定係数なのです。
統計検定2級における単回帰分析の問題
統計検定2級における、回帰分析の問題としては、実際に1から回帰直線や回帰式を求める問題は出題されません。
そもそもpythonやエクセルなど、各種ツールを使わないと解くのは現実的ではありません。
出題パターンとしては、以下のような形で出題されます。
単回帰分析の例題
アンケート調査で、社会人の偏差値と収入のデータをとり、収入を目的変数、偏差値を説明変数とした単回帰モデルを考える。
$y=β_0+β_1x+u$
上記のモデルを、最小2乗法で推定したろころ、下記の結果となった。
結果をもとに、以下の問いに答えよ。
| 回帰係数 | 標準誤差 | t値 | P値 | |
| 切片 | -296.8523 | 61.662 | -4.814 | 0.001 |
| $x(偏差値)$ | 14.2614 | 1.160 | (A) | 0.000 |
- 偏差値が1上がると収入が14.2614上がると言えるか?
- (A)に入る数値を小数点第2位まで求めよ
- 偏差値が60だった場合の収入の推計値を求めよ
このような形で出題されることがあります。
まず、表のそれぞれの意味を理解しましょう。
回帰係数
回帰係数とは、説明変数と目的変数の相関関係を示す統計量です。
回帰係数は、説明変数が1単位変化したときに目的変数がどれだけ変化するかを表します。回帰係数は、正の値の場合は説明変数と目的変数が正の相関関係にあり、目的変数が説明変数が増加するにつれて増加します。
回帰係数が負の値の場合は説明変数と目的変数が負の相関関係にあり、目的変数が説明変数が増加するにつれて減少します。
標準誤差
単回帰分析における標準誤差とは、回帰係数のばらつきを表す統計量です。
標準誤差は、回帰係数が真の値からどの程度離れているかを表します。
標準誤差が小さいほど、回帰係数が真の値に近いことを意味します。
標準誤差は、単回帰分析において、回帰係数の信頼性を評価するための重要な統計量です。標準誤差が大きい場合は、回帰係数が真の値から離れているため、回帰係数を信頼することはできません。
標準誤差が小さい場合は、回帰係数が真の値に近いため、回帰係数を信頼することができます。
t値
t値とは、回帰係数の統計的有意性を示す統計量です。
t値が大きいほど、説明変数が目的変数に与える影響が大きいです。
t値は、回帰係数の予測を行う際にも使用されます。t値が大きいほど、回帰係数は信頼性が高く、目的変数の予測値も正確になります。
目安として、t値の絶対値が2よりちいさいと、その説明変数は目的変数に影響しないと判断されます。
t値は以下の式で求めることができます。
$t値= 回帰係数÷標準誤差$
P値
単回帰分析におけるp値とは、回帰係数が0であるという帰無仮説が真である確率です。
p値が小さいほど、回帰係数が0ではないという対立仮説が真である可能性が高くなります。
p値が有意水準(通常は0.05)以下であれば、回帰係数が0ではないという対立仮説が採用されます。
p値は、単回帰分析において、回帰係数の有意性検定を行う際に重要な統計量です。p値を用いて、回帰係数が0であるという帰無仮説が真であるかどうかを判断することができます。
たとえば、回帰係数のp値が0.01であれば、回帰係数が0であるという帰無仮説が真である確率は1%です。つまり、99%の確率で、回帰係数が0ではないという対立仮説が真であると言えます
例題の答え
では実際に、上記の例題の答えを見ていきましょ。
①偏差値が1上がると収入が14.2614上がると言えるか?
いきなり答えを言ってしまうと、「言える」が答えです。
回帰係数は、説明変数が1単位変化したときに目的変数がどれだけ変化するかを表していますので、偏差値が1上がると、収入が「14.2614」上がることが分かります。
②(A)に入る値を小数点第2位まで求めよ
t値を求めるには、回帰係数÷標準誤差をすれば良いのでした。
以下の式で求めることができます。
$t値= 14.2614÷1.160=12.29$
③偏差値が60だった場合の収入の推計値を求めよ
回帰式から求めることができます。
回帰式は$y=β_0+β_1x$でしたね!
結果の表から、
- $β_0=-296.8523$
- $β_1=14.2614$
ということが分かっています。
そして、$x=60$を代入して計算します。
$y=-296.8523+14.2614×60=558.8317$
このように、回帰式を使うことで簡単に求めることができます。
Work illustrations by Storyset














