なぜビジネスに統計学が必須なのか？データサイエンティストが教える真実

ひろゆきや石丸市長はなぜディベートに強いのか？

その背景には統計学に基づいた分析を行い、どちらが良いのか数字的に判断しているからです。

ひろゆき氏は議論の中でしばしば客観的なデータや事例を持ち出し、感情的な議論ではなく論理的な議論へと話を引き戻します。また、石丸市長も政策の提案や市民との対話において、具体的なデータや根拠を提示することで説得力を高めています。

なんの事はありません。統計的に見て、1%でも確率が高いと判断した方を支持しているのです。

一方論破される側は数値的根拠無く、あくまで自身の主観で物事を語ってしまい論破されてしまうのです。

これはビジネスシーンにおいても非常に重要です。

あなたの周りにもいないでしょうか？
データを見たときになんとなくこうだろうと、自身の勘や経験を基に結論づけてしまう人や、自身の都合の良いように解釈をしてしまう人を。
そうならないためにも、大切なのは統計学を用いてデータを分析することです。

今回の講座ではなぜビジネスに統計学が必要なのか？
その点を深堀りしていきます。

 

統計学とは何か？

ひとくちに統計学と言っても色々ありますが、まず抑えておきたいのが以下の2つです。

簡単にですが、それらが何か解説します。

 

記述統計学

記述統計学とは、収集されたデータを要約し、その特徴を数値やグラフで表現する統計学の一分野です。いわば、データの全体像を把握するための羅針盤のようなものです。

具体的なものとしてはこれらのものがあります。

ではビジネスにおいて、記述統計学がなぜ必要なのか？
それは主に以下の3点です。

 

 

推測統計学

推測統計学はその名の通り、一部のデータから全体を推測する統計学です。
まさに占い師ですね！

例えば、顧客全員にアンケートを取るのはコストが掛かりすぎて現実的では無いことも多いでしょう。
そんな時に一部の顧客にだけアンケートを取り、そのデータから全体を推測するのが推測統計学です。

また、ある施策を試した時に売り上げが100万円から105万円に上がったとします。
これが本当にその施策の効果であったのか？はたまた偶然だったのかを判別します。

まとめると、ビジネスにおいて推測統計学は以下のメリットがあります。

 

ビジネスで使える統計的手法

では一気に実践的な話をします。
具体的に、ビジネスシーンで使える統計的手法を解説します。

色々あるのですが、まずは代表的な以下の手法を解説します。

 

 

Z検定

Z検定は、正規分布に従う母集団の平均値を検定するための統計学的手法です。
簡単に言うと、ある集団の平均値が、または別の集団の平均値と統計的に有意な差があるかどうかを調べます。

こういうとザ・統計学といった感じで難しく感じてしまいますよね。
分かりやすくするために以下のシーンで考えてみましょう。

これは実際にもあり得るシーンですよね？
本当に画像を変えた効果によるものなのか？それともたまたま偶然上がったのか？判別が難しいと思います。
このような2群の比率差の検定で使えるのがZ検定なのです。

Z検定に関しての詳細は割愛しますが、pythonを使うと以下のコードで検定をする事ができます。

->0.3080848594337397

上記の結果、P値と呼ばれるものが0.308~という数字になりました。

これが何を表しているのか簡単に言うと、まずP値とは値が小さいほど、その値となることはあまり起こりえないことを意味しています。
つまり今回の場合は、30％の確率でこの確率が得られることを示しています。
画像を変えていなかったとしても30%の確率で5.5%のクリック率になっていたと考えられます。
また、統計学では効果があったのかの判断基準(有意差)として一般的に0.05以下の場合としています。

ですので、今回の場合はP値が高いために、画像を変えた結果クリック率が上がったと結論づける事は出来ないのです。

 

t検定

つづいてt検定です。
t検定は非常に良く使う検定でして、平均値差の検定で使われます。
つまり2つの集団があるとして、その平均値に差があるのか？それを検定するイメージです。

例えば、以下のシーンを想像してください。

このようなシーンでt検定がいきてきます！

今回は有名なデータセットのtipsというものがseabornライブラリにありますので、そちらをサンプルにしています。

まずtipsというデータセットがどういうものかと言うと、以下のようなデータセットとなっています。

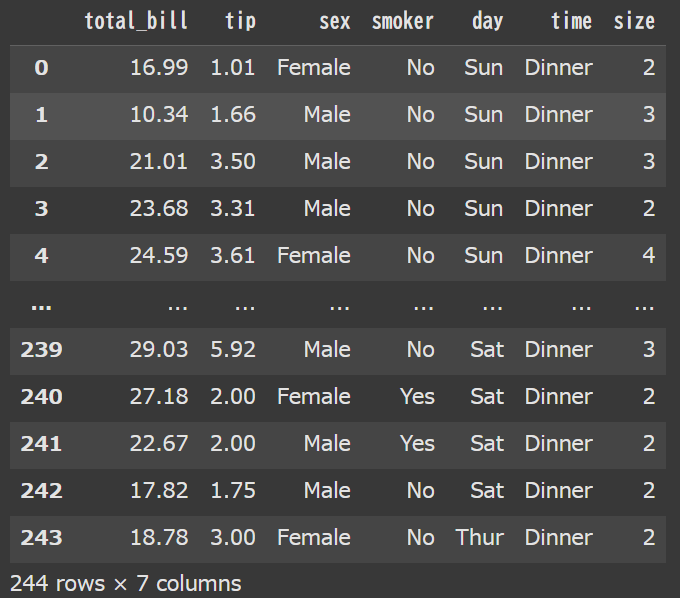
total_billという列が支払い金額で、sex列が性別ですね。Maleが男性でFemaleが性別を表しています。ちなみに単位はドルです。
それぞれの性別毎のtotal_billの平均を求めた結果が以下になります。

• Male = 20.744
• Female = 18.056

このように、約2.7ドルほどMaleの方が高い結果となりました。
しかしこれだけで性別によって差があると結論づけて良いのでしょうか？
しかもデータは244回の会計記録だけです。

こんな時統計学ではt検定を行い、平均値差の検定を行います。
詳しい数式は省きますが、Pythonでは以下のコードで検定を行う事ができます。(厳密にはウェルチのt検定を行っています)

->pvalue=0.0185733948549217

結果P値が0.018となりました。
これは0.05よりも小さいので、男女のtotal_billの平均には差があると言って良さそうだということが分かります。

 

相関係数

相関係数も非常に重要です。

相関係数とは、2つのもの（変数）がどれくらい関係しているかを表す「関係の強さと方向」を示す数字です。
ちなみに変数とは先ほどのデータセットのtotal_billやtipなどの列にあたる部分です。
簡単に言うと、「片方が変わると、もう片方はどう変わるか」を調べるための指標です。

特長としてはこれらがあげられます。

例えば、身長と体重などはイメージしやすいでしょう。
平均的に身長が高い人ほど、体重も増えるというのは理解できますよね？
このような場合を正の相関と言い、関係も強い事が分かります。

ではビジネスシーンで考えてみましょう。

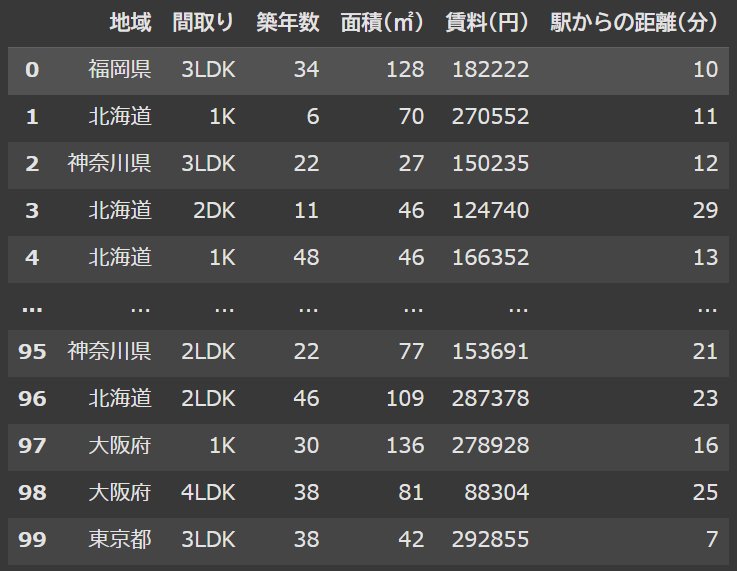
不動産のシーンを例に、上記のようなデータセットがあったとします。
地域や間取り、築年数など(変数)の情報から適切な賃料(円)を予測出来そうですよね？

また、色々ある変数の中でどれが一番賃料に影響するのかを知りたいって時に相関係数が重要になるのです。

例えば相関係数が以下のようになったとします。

この場合面積と賃料は相関係数が+1に近いためそこそこ正の相関が強いことが分かります。
つまり、面積が広ければ広いほど、賃料が上がると言えそうです。
また逆に、築年数や駅からの距離に関してはそこまで-1に近いわけではありませんが、負の値をとっています。
このような場合、負の相関となり、築年数が多ければ多いほど賃料が下がっていく関係という事が分かります。

今回は分かりやすい変数を使っているので、「そりゃそうだろう！」と思うと思います。
しかし、実際の現場では意外な変数が重要であったという事も往々にしてありますので、相関係数も非常に重要です。

 

回帰分析で未来を予測

ここまでの話しでは取得したデータをこねくり回して、なんとかして特徴を掴もうとする、あくまで過去に対する話しでした。
しかし、ビジネスシーンで大事なのは未来に向けて予測する事ですよね？

小売り業なら、商品の販売数を予測して在庫を持ちますし、上記のような不動産の場合は適切な賃料を設定して契約してもらいたいですよね？

このように、未来を予測する時に使うのが回帰分析です。

またまた不動産の例をもとに話します。

先ほど、面積と賃料はそこそこ強い正の相関があり、築年数は負の相関があることを話しました。
このように、各列の情報から考えていけば適切な賃料も予測する事が出来そうですよね？
ちなみに各列のことを先ほどは変数と言いましたが、回帰分析など機械学習の分野では特長量と言います。(めんどくさいですね、、)

ちなみに一つの特長量から予測する事を単回帰分析と言います。
例えば、面積の情報だけで賃料を予測する場合などが単回帰分析です。
逆に複数の特長量から予測する場合は重回帰分析と言います。
面積、築年数、駅からの距離など複数の情報から賃料を予測する場合ですね。

ちろんですが、重回帰分析の方が計算量は増えますが予測精度は高くなります。
実際の現場でも使われるのは重回帰分析がほとんどでしょう！

 

長くなりましたが、このように統計学を活用するとビジネスシーンでも非常に有効な場面が多いです。
というか、統計学を分かっていないと正しい判断が出来ない場面も非常に多いので是非活用してもらいたいと思います。

 

単回帰についてより深く知りたい人は↓

【わかりやすい】単回帰分析とは何か？実務で使えるシーンを紹介！統計検定を受験する！仕事でデータ分析してると回帰分析が大事って聞くけどどういう物なの？今回はそんな疑問に答えます！ この様...