ど～も、データサイエンティストのえいせいです。
今回は、Pythonで簡単にできる統計手法「t検定」について、初心者の方にもわかりやすく解説していきます！
- 「t検定って聞いたことあるけど、難しそう…」
- 「データ分析に使えるって言われても、どうやればいいの？」
そんなあなたのために、理論もコードもわかりやすく、そして実際にPythonで動かしながら解説していきます！
t検定とは？
まずは「t検定とは何か？」をざっくり説明します。
t検定は、2つの平均値に差があるかどうかを調べる統計手法です。
例えば以下のような場面で、平均値に差があるのかを調べられます。
- 新しい薬が従来の薬より効果があるか？
- 東京と大阪で平均身長に差があるか？
例えば東京と大阪で各10人の身長を測り、平均を出した結果が以下の通りになったとします。
| 平均身長 | |
| 東京 | 170cm |
| 大阪 | 174cm |
この結果をみて大阪の方が身長が高いと言い切ってしまって良いのでしょうか？
10人だけの結果だと、たまたまという事もあり不安ですよね～！
では100人、1000人と増やした結果だったらどうでしょう？
信頼度は増えますが、どのタイミングで平均に差があると言って良いのか迷いますよね～！
そういった問題を、t検定を使う事で解決する事が出来ます！
t検定は2種類ある
t検定には以下の2種類があります。
- 対応のないt検定（独立2群）：異なるグループを比較
- 対応のあるt検定（対応あり）：同じ人に2つの処置をしたときの比較
対応のないt検定
例えばAグループとBグループからサンプルデータを採取するなど、全くの別人からデータを取得する時がそれにあたります。
対応のあるt検定
2つのサンプルが同じ対象に対して2回測定されたデータです。
例えば、新しい教育プログラム導入前後でのテスト成績を同じ生徒で採取したり、ダイエット前後の体重変化を同じ人から採取する場合がそれにあたります。
t検定の数式
またt検定といっても、ウェルチのt検定やスチューデントのt検定など色々あり、求めるための数式が若干違います。
しかし、現在では等分散である必要がない、かつ計算リソースが増えてもツールがあれば簡単に求める事が出来るため、ウェルチのt検定を使う事が一般的です。
※ちなみに等分散の意味が分からなくても今回の内容は全く問題ありません。
ウェルチのt検定の数式は以下になります。
\[
t = \frac{\bar{X}_1 – \bar{X}_2}
{\sqrt{ \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} }}
\]
各記号の意味
パッと見ですと難しい数式に感じるかもしれませんが、各記号の意味が分かれば理解できると思います。
\[
\begin{array}{l}
\bar{X}_1,\ \bar{X}_2 = \text{それぞれのサンプルの平均値} \\
s_1^2,\ s_2^2 = \text{それぞれのサンプルの分散（不偏分散）} \\
n_1,\ n_2 = \text{それぞれのサンプルサイズ（データ数）} \\
t = \text{t値（統計量）} \\
\end{array}
\]
ただこの数式を覚える必要は全くありませんので、この様にして求めた結果、t値というのが求まるんだな～という理解で大丈夫です。
t値とp値と有意差の考え方
t検定の流れとしては、詳しい求め方は割愛しますが上記で求めたt値と自由度からp値を求め有意差があるか判定します。
自由度とは各グループのサンプルサイズ(標本の数)と不偏分散から求める事が出来ます。
具体的には以下の式から求められます。
\[
df = \frac{
\left( \dfrac{s_1^2}{n_1} + \dfrac{s_2^2}{n_2} \right)^2
}{
\dfrac{ \left( \dfrac{s_1^2}{n_1} \right)^2 }{n_1 – 1}
+ \dfrac{ \left( \dfrac{s_2^2}{n_2} \right)^2 }{n_2 – 1}
}
\]
各記号の意味
\[
\begin{array}{ll}
s_1^2,\ s_2^2 & : \text{それぞれの標本分散（不偏分散）} \\
n_1,\ n_2 & : \text{それぞれの標本サイズ（データ数）} \\
df & : \text{自由度}
\end{array}
\]
数式は一見複雑ですが、各群の標本サイズと不偏分散が分かれば求める事が出来るのでそこまで難しくありません。
また覚える必要もありませんので、「こういう感じに求めてるんだ～」位に捉えてください。
逆に大事な事として、t検定では以下の流れで判定するという事は覚えておきましょう。
- t値を求める
- t値と自由度からP値を求める
- p値から有意差があるか判定
ここでちょっと大事な理論、p値と有意差について説明します。
統計学などでは一般的にp値が0.05以上かどうか？を見ます。
-
p値 < 0.05 → 有意差がある（差が「偶然」である確率が5%未満）
-
p値 >= 0.05 → 有意差がない（差は偶然の可能性が高い）
上記のように、p値が0.05より小さい場合、それが起こる確率は5％未満であるため平均値には有意に差があると判断されます。
逆に0.05以上の場合は、偶然の可能性もあり、十分に起こりうる範囲とし、2つの平均に有意な差があるという証拠が不十分であることを意味します。
ちょっと難しいと感じるかもしれませんが、シンプルに考えて「P値が0.05未満だったら平均に差がある。0.05以上だったら差があると言えない。」と覚えてください。
ちなみに基準値を0.05に設定するのが一般的ですが、より厳しく判定したいなどで、0.01等とする場合もあります。
Pythonの準備
t検定の概要が分かったところで、次はPythonで実装していくための準備をしていきましょう。
すでに環境が整っている方はそちらを使えば良いのですが、まだ無いという人は1から作るとなると少し手間ですので、google colaboratoryでサクッと試しましょう。
googleアカウントがあれば無料で実行できる環境が整っています。
しかもAI付なので、プロンプトで一瞬でコードを書いてくださるという神対応もしてくれます。
google colaboratory：こちらからアクセスすればすぐに使えます！
また、Pythonでt検定を行うためには、以下のライブラリを使います。
|
1 2 3 4 |
import numpy as np import pandas as pd from scipy import stats import matplotlib.pyplot as plt |
これらは基本的なライブラリなので、google colaboratoryには既にインストールされていますが、無いよって人にはpip installで簡単にインストールできます。
|
1 |
pip install numpy pandas scipy matplotlib |
対応のないt検定をPythonで実装
ではまず対応のないt検定をPythonで実装してみましょう。
「AクラスとBクラスでテストの平均点に差があるのか？」
各5人のテスト結果を変数a_classとb_classに入れて検定してみます。
この時SciPyライブラリのstatsモジュールにあるttest_ind関数をを使います。
この関数は引数でequal_var(等分散)をFalseにしてあげる事でウェルチのt検定となります。戻り値としてt値とp値を返すので、その値を確認しましょう。
|
1 2 3 4 5 6 7 8 9 |
# AクラスとBクラスのテスト結果 a_class = [65, 68, 70, 72, 71] b_class = [75, 78, 74, 73, 77] # t検定 t_stat, p_value = stats.ttest_ind(a_class, b_class, equal_var=False) print("t値:", t_stat) print("p値:", p_value) |
t値: -4.0020827910809995
p値: 0.0039383091001110124
コードを実行すると、このような結果となりました。
重要なのがp値であり、この値が0.05を下回るかどうかが重要でしたね！
今回は0.0039と下回っているので、平均に差があるとみて良さそうです。
Pythonを使えばこのようにしてt検定を行う事が出来ます。
非常に簡単ですね～！
ちなみに各クラスの平均値は以下のコードで見ることができます。
|
1 2 |
print(np.mean(a_class)) print(np.mean(b_class)) |
69.2
75.4
また結果をグラフにしてみましょう。
今回は箱ひげ図です。
|
1 2 3 |
plt.boxplot([a_class, b_class], labels=["a_class", "b_class"]) plt.title("a_class vs b_class") plt.show() |
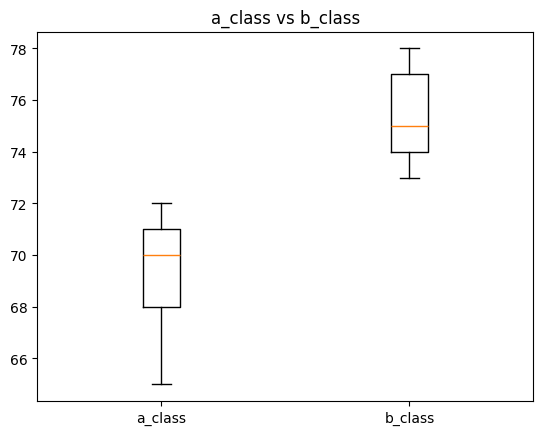
点数差がある事が視覚的に分かりますね！
対応のあるt検定
次は「対応のあるt検定」です。
これは「ダイエット前と後で体重に差があるのか？」のように、同一人物の比較に使います。
また、先ほどまでは直接listを作成して比較していました。
しかし、実践の場面で手で直接listを作る事はそんな多くないでしょう。
数字を手打ちするのは面倒ですし、実務ではデータの数が何千、何万とあるのが普通ですからね。
csvファイルにデータセットがあると仮定してやってみましょう。
まずはダイエット前(before)と後(after)のデータをランダムに100個作り、それをcsvファイルで出力します。
今回は有意差が出る様にデータを作ります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# prompt: 以下のdataframeを作成し、csvとして出力するコードを書いてください。 # カラムはbeforeとafterの2つ。レコードは100です。数値は整数としてください。 # これは、ダイエットの前と後の体重を測ったデータで、t検定で有意差が出る数字でお願いします。 import pandas as pd import numpy as np # 平均値が異なる2つのグループのデータを生成 (t検定で有意差が出るように) np.random.seed(0) # 再現性のためにシードを設定 before = np.random.normal(loc=70, scale=10, size=100).astype(int) after = np.random.normal(loc=65, scale=10, size=100).astype(int) # DataFrameの作成 df_weight = pd.DataFrame({'before': before, 'after': after}) # CSVファイルとして出力 df_weight.to_csv('weight_data.csv', index=False)こ |
このようにする事でweight_data.csvファイルが作成されたと思います。
では続いて、このcsvファイルを読み込み中を見てみましょう。
|
1 2 3 |
# CSVファイルの読み込み df = pd.read_csv('weight_data.csv') df |
100人分のダイエット前と後のサンプルデータが無事作成されている事が分かりますね。
ではそのままbeforeとafterで対応のあるt検定を行ってみましょう。
今度はstatsモジュールのttest_relを使います。
|
1 2 3 4 5 |
# 対応のあるt検定の実行 t_stat, p_value = stats.ttest_rel(df['before'], df['after']) print(f"t値: {t_stat}") print(f"p値: {p_value}") |
t値: 3.4712750818627733
p値: 0.0007691439129912855
結果、p値が0.05を下回っているので有意差がある事が分かりました。
両側検定と片側検定
ちなみに検定には両側検定と片側検定があります。
上記のコードでは両側検定を行っていました。
それぞれの意味としては以下の通りです。
| 検定の種類 | 見ている差 | 使う場面 |
|---|---|---|
| 両側検定 | 上か下か、どちらの方向でも差があればOK | 「差があるかどうか」だけを知りたいとき |
| 片側検定 | 一方の方向の差だけを見る | 「○○が大きい」「○○が小さい」と方向に注目したいとき |
上記のコードですと、体重に差があるとどうかを検定した結果となっています。
極論、逆に全員体重が増えた場合も有意差があるとなってしまいます。
しかし、実際にはダイエットのデータなので、beforeよりafterが下がっているかが大事ですよね？
こんな時は片側検定を行います。
stats.ttest_rel関数の引数にalternativeがありますので、以下のどちらかを指定すればOKです。
- greater：1つ目で指定したデータの方が大きいか？
- less：1つ目で指定したデータの方が小さいか？
この引数を指定してみましょう。
|
1 2 3 4 5 |
# 対応のあるt検定（片側検定） t_stat, p_value = stats.ttest_rel(df['after'], df['before'], alternative='less') print(f"t値: {t_stat}") print(f"p値: {p_value}") |
t値: -3.4712750818627733
p値: 0.00038457195649564273
第一引数をafterにし、こちらの方が低いかを見るためにalternative=’less’とする事で片側検定を行っています。
片側検定の結果も有意差があるという事が分かりましたね！
まとめ
今日のまとめ！
- t検定は2つの平均値の差を調べる統計手法
- Pythonではscipy.statsを使えば簡単に実行できる
- t検定には2種類ある
- 対応なし(独立2群)
- 対応あり(同一人物の比較)
t検定をマスターすると、マーケティング・教育・医療・ビジネス分析などあらゆる分野に応用できます！
ぜひ、今日のコードを参考に、自分のデータでも試してみてくださいね！
