この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 箱ひげ図って何?
- 四分位数が良く分からない?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回は箱ひげ図について、どこよりも分かりやすく解説していきます。
箱ひげ図とは?
初めて聞いた人も多いでしょう。
まず箱ひげ図とは以下の様な物を指します。
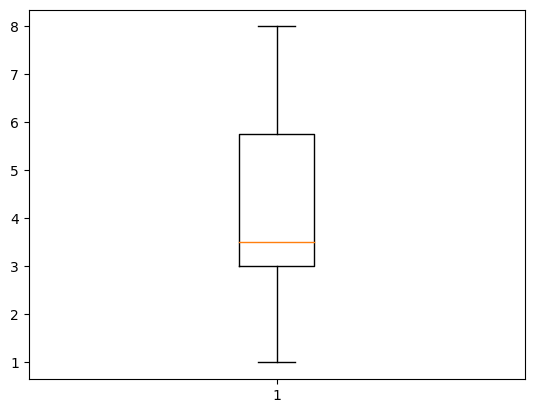
[1, 2, 3, 3, 3, 4, 5, 6, 7, 8]このデータセットをプロットしています。
箱ひげ図は、データセットの分布を視覚化するのに役立つ統計グラフです。
データセットの中央値、四分位数、および外れ値を表示するために使用されます。
箱ひげ図は、データを簡単に比較したり、データの異常を特定したりするために使用されます。
箱ひげ図の見方

箱ひげ図という名前だけに、まずは以下のポイントを抑えておきましょう。
- 箱:真ん中の箱の部分
- ひげ:上下に伸びる黒い線
単純で分かりやすいですね!
また、ひげの下端は最小値の1を示しており、上端は最大値の8を示しています。
しかし、外れ値検出する場合はこの表記ルールが変わりますので注意してください。(詳しくは後述します。)
四分位数とは?
箱ひげ図を読み解く上で、絶対に必要なのが四分位数です。
四分位数は、データを小さい順に並べたときに、データの数で4等分した時の区切り値です。
4等分すると3つの区切りの値が得られ、小さいほうから以下の様に呼びます。
- 第一四分位数:25パーセンタイル
- 第二四分位数:50パーセンタイル(中央値)
- 第三四分位数:75パーセンタイル
また、75パーセンタイル(第三四分位数)から25パーセンタイル(第一四分位数)を引いた値を「四分位範囲」とよびます。
先ほどの箱ひげ図で表すと↓の様になります。
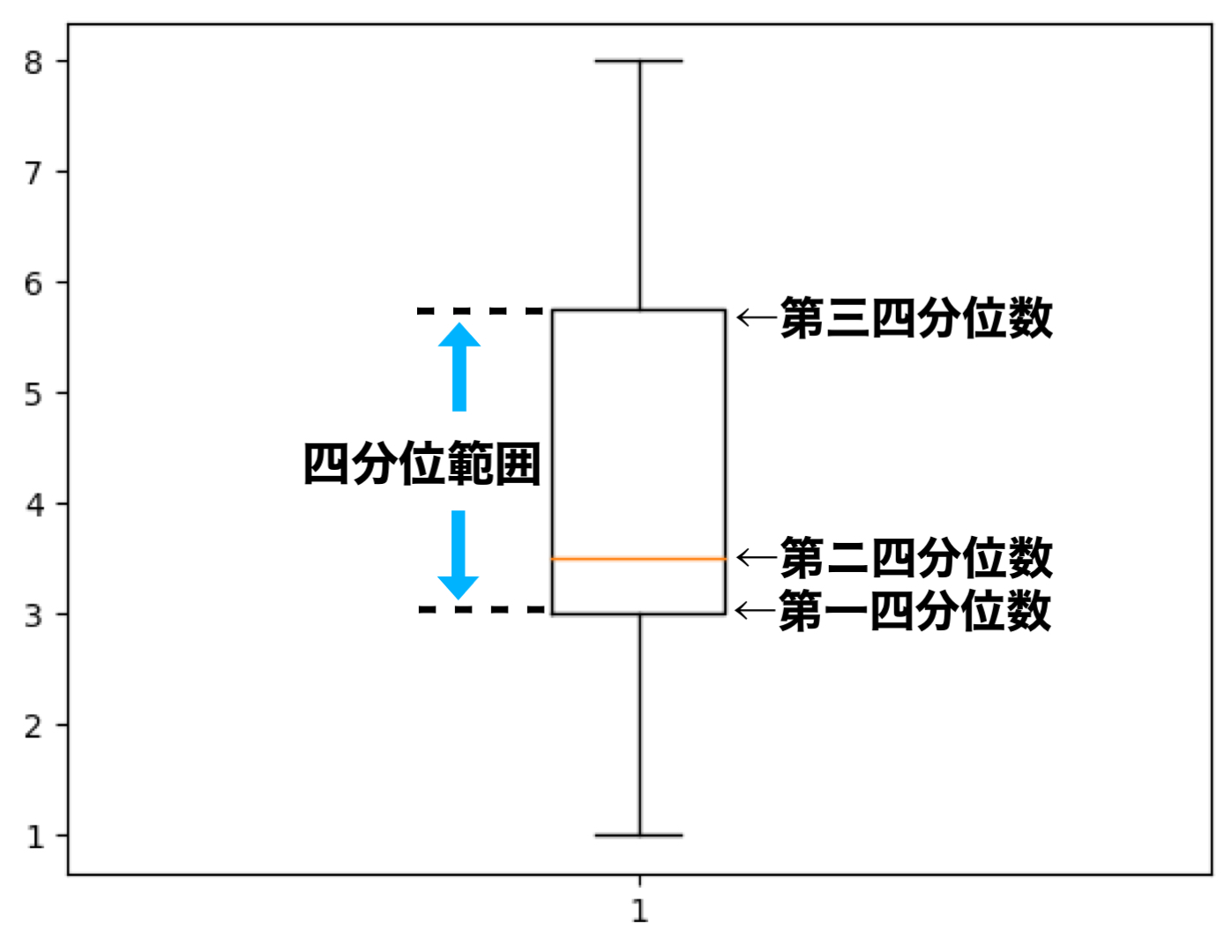
箱ひげ図は4つに区切れる
要は、第二四分位数(中央値)を中心に、4つのブロックにデータを区切ったのが箱ひげ図です。
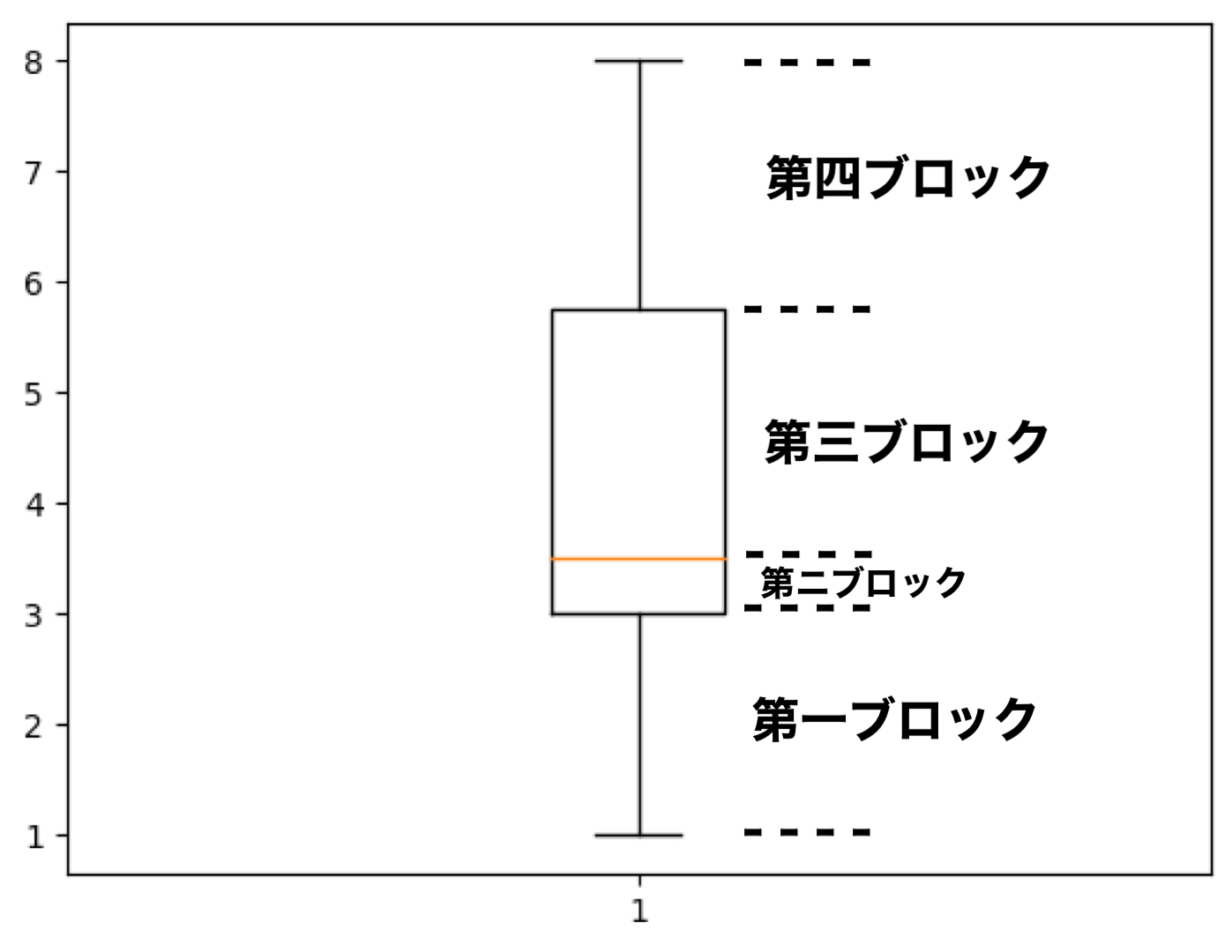
大事なポイントとして、各ブロックに入っているデータの数は同じです。
しかし、ブロックごとにデータの大きさが違うのはデータのバラつきを表しています。
この箱ひげ図から得られる情報としては↓の物があります。
- 第一四分位数と第二四分位数の間の第二ブロックは、箱がコンパクトな事からデータがまとまっている(ばらついていない)事が分かる
- その他のブロックは大きさが同じなので、バラつき具合は似ている
- 最小値が1で最大値は8
- 四分位範囲に全体の半分のデータが入っている
外れ値検出する場合の箱ひげ図
箱ひげ図では外れ値があった場合、それを分かりやすくプロットする事ができます。
ようは、外れ値をひげの範囲外に○や×で表示してくれるのです。
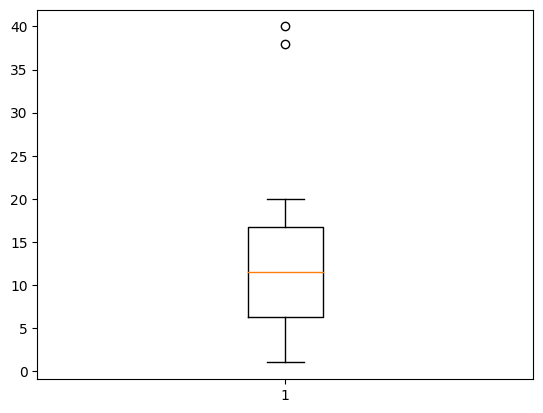
この様に表記する事で「外れ値がどれくらいあるのか?またその値はどれくらいなのか?」という点を視覚的に分かりやすくしてくれるので、重宝します。
また、この際重要になってくるのが、どこまでをひげの範囲とするか?です。
なんとなくで決めるわけにはいきません。
箱ひげ図のひげの範囲
簡単に説明すると以下の範囲です。
上限方向と下限方向の2つがあります。
- 第一四分位数-1.5×四分位範囲
- 第三四分位数+1.5×四分位範囲
この様に範囲を決める事ができます。
ちなみに1.5の数値は変わる事があります。
データセットによっては1.7にしたりと変化しますが、1.5が一般的です。
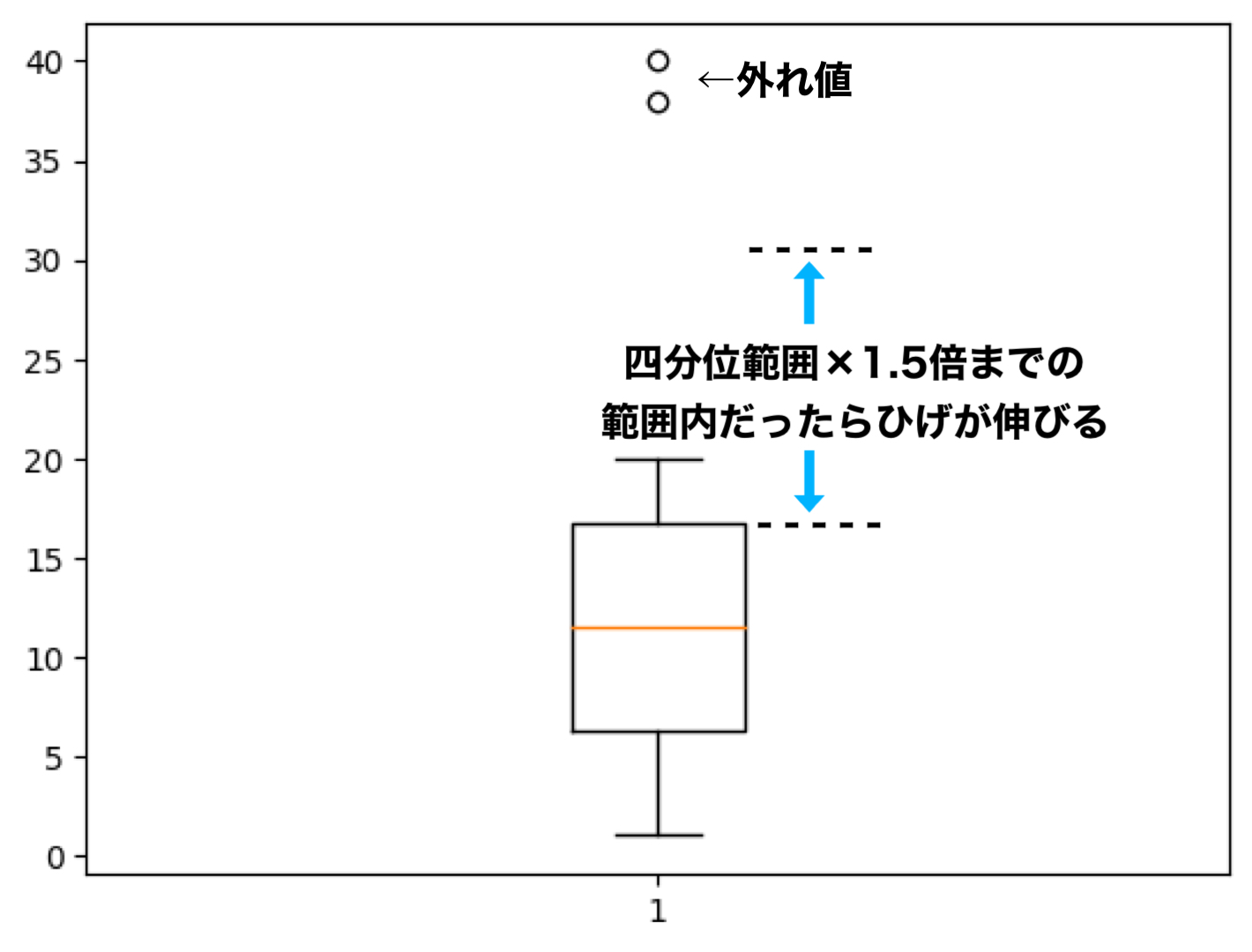
注意点としては、今回は外れ値以外での最大値が20まででしたのでひげが20までしか伸びていません。
もちろん下限もありますので、第一四分位数-1.5×四分位範囲よりも小さい値は外れ値となります。
詳しい数値の求め方は次のセクションで説明します。
箱ひげ図の作成方法
箱ひげ図を作成する際の流れです。
- データを昇順(小さい順)にソートする
- 第二四分位数(中央値)を求める
- 第一四分位数と第三四分位数を求める
- 箱ひげ図を描画する
下記の15個のデータセットを使い、描画してみましょう。
ソートする
まずはデータを昇順に並び替えます。
$[22, 42, 44, 44, 47, 49, 50, 51, 52, 53, 54, 58, 60, 65, 75]$
第二四分位数(中央値)を求める
[22, 42, 44, 44, 47, 49, 50, 51, 52, 53, 54, 58, 60, 65, 75]
今回は奇数個なので、単純に中央値である51になります。
偶数個の場合は、真ん中になる2つの値の平均値が中央値になるんでしたね!
第一四分位数と第三四分位数を求める
まずは第二四分位数(51)よりも数字が小さいグループと多きグループに分けます。
- 小さいグループ:$[22, 42, 44, 44, 47, 49, 50]$
- 大きいグループ:$[52, 53, 54, 58, 60, 65, 75]$
その中で先ほどと同じ様に、中央値を求めます。
それが第一四分位数と第三四分位数になります。
小さいグループ:$44$ ←第一四分位数
大きいグループ:$58$ ←第三四分位数
これで全ての四分位数が分かりましたね!
箱ひげ図を描画する
最後に描画して終了です。
基本的に描画は各種ツールを使用して描画します。
描画までは統計検定では出題されないので、安心してください。
ちなみにpythonでは下記のコードで描画できます。
|
1 2 3 4 5 6 7 8 9 |
import matplotlib.pyplot as plt # データの作成 data = [44, 47, 58, 42, 60, 22, 44, 52, 75, 51, 50, 65, 53, 54, 49] # 箱ひげ図の作成 plt.boxplot(data) plt.show() |
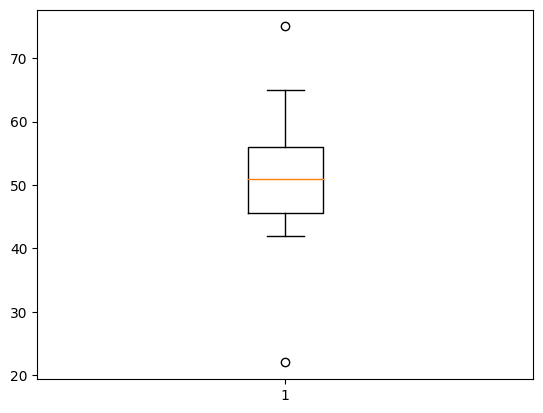
箱ひげ図の注意点
では最後に箱ひげ図の注意点を抑えておきましょう。
- データの分散や歪みを視覚化することはできない
- データの比較にも使用できるが、データが異なる尺度で測定されている場合は、正確に比較できない可能性がある
- データが正規分布していない場合は、データの分布の形状を正確に表していない可能性がある
これらの注意点を認識しておけば、箱ひげ図はデータの分布を視覚化するための貴重なツールとなります。
練習問題
以下の図は、日本の五か所の気温のサンプルデータでを箱ひげ図で表したものである。
各問いに答えなさい。
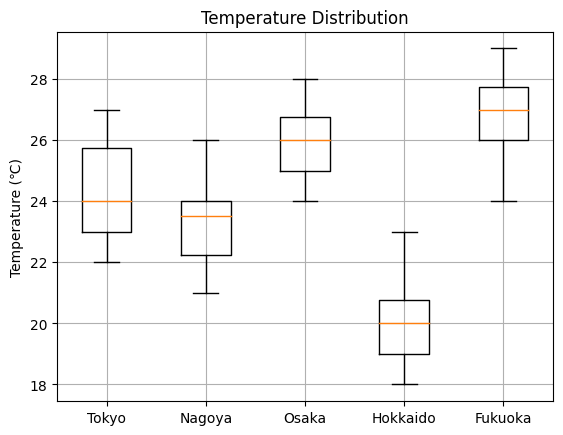
第一問
- [21, 22, 22, 23, 23, 24, 24, 24, 25, 26]
- [24, 25, 25, 25, 26, 26, 26, 27, 27, 28]
- [22, 22, 23, 23, 24, 24, 25, 26, 26, 27]
- [18, 18, 19, 19, 20, 20, 20, 21, 22, 23]
- [24, 25, 26, 26, 27, 27, 27, 28, 28, 29]
答え:③
第二四分位数(中央値)に着目してみると簡単です。
中央値が24になるデータは③だけです。
第二問
- 平均気温が一番高いのは大阪である。
- 四分位範囲が一番大きいの北海道である。
- 福岡の第一四分位数は26である。
答え:③
- 第二四分位数(中央値)が一番高いのは福岡です。
- 四分位範囲とは第三四分位数から第一四分位数を引いた範囲で、一番大きいのは視覚的にも東京です。
- その通りです。














