この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 棒グラフとか折れ線グラフってどんな時に使うの?
- 散布図ってなに?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回の講座では検定で必要な各種グラフに関する知識をマルっと教えます。
棒グラフ、折れ線グラフ、散布図に相関図と幅広い内容になっています。
棒グラフとは?
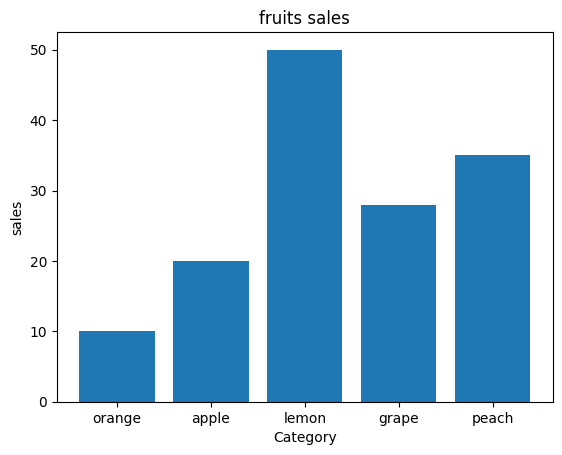
この様なグラフを棒グラフと言います。誰しもが一度は見たことがあると思います。
棒グラフは、さまざまなカテゴリの間の数値の比較を示すために使用されるタイプのグラフです。
棒グラフの使用例
棒グラフは、以下の様な場合に使われる事が多いです。
- さまざまな年齢層の人口統計
- 製品の売上
- 学校の成績
たとえば、棒グラフを使用して、さまざまな年齢層の人口統計、さまざまな製品の売上、さまざまな学校の成績など、さまざまなカテゴリ間の数値の比較を示すことができます。
棒グラフは、データを視覚化する簡単でわかりやすい方法です。また、データを簡単に比較できるため、データを説明するのに適しています。
棒グラフの注意点としては、カテゴリーの数が多くなると分かり辛くなります。
20個、30個とあると視覚的に捉えるのが難しくなるので注意しましょう。
折れ線グラフとは?
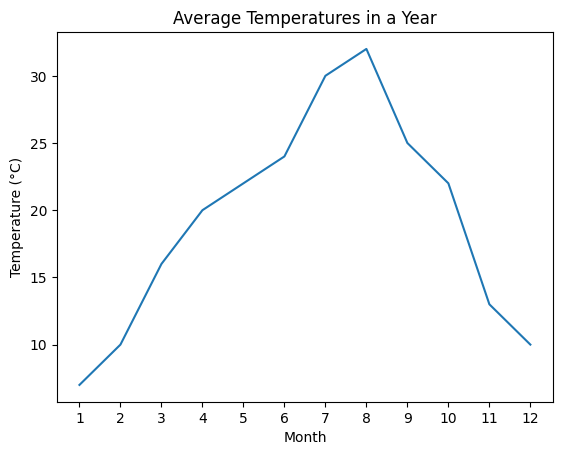
これも見た事がある人が多いと思います。
折れ線グラフは、データの値の時間の経過にわたる変化を示すために使用されるタイプのグラフです。
特に下記のシーンで使われる事が多いです。
- 時間の経過にわたる売上
- 日時による温度の変化
- 株価の推移
円グラフとは?
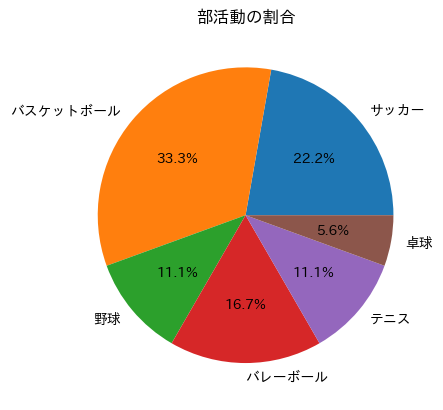
円グラフは、データセット内のカテゴリの相対サイズを示すグラフです。円をいくつかの扇形に分割し、各扇形はデータセット内のカテゴリを表します。
扇形のサイズは、カテゴリのサイズに比例しています。
円グラフの使用シーン
- 顧客ベースの性別分布
- 従業員の部門別分布
- 製品の売上高の地域別分布
- 使用デバイスの割合
これだけに留まらず、カテゴリの割合を示す場合には幅広いシーンで使う事ができます。
逆に、時間の経過の変化を表す際やカテゴリの絶対値を示す際にはあまり適していません。
クロス集計表
| 映画 | 買い物 | カラオケ | ダーツ | 合計 | |
| 男 | 22 | 15 | 38 | 25 | 100 |
| 女 | 17 | 38 | 34 | 11 | 100 |
| 合計 | 39 | 53 | 72 | 36 | 200 |
クロス集計表は初めて見たという人も多いかもしれません。
上記の例では男女別の趣味の分布をクロス集計にしました。
クロス集計表の説明
クロス集計表は、2つの変数間の関係を示すために使用される表です。
変数ごとに1つの列と1つの行があり、各セルには2つの変数の組み合わせの頻度が表示されます。
つまり、2つの変数間の関係を理解するための強力なツールなのです。
また、上記の例では行には男女の2カテゴリーが入っており、列には趣味の4カテゴリーが入っています。
そのため「2×4のクロス集計表」と呼ばれます。
覚えておきたい専門用語としては↓の物があります。
- 表側(表側):行の項目。黄色の部分。
- 表頭(表頭):列の項目。水色の部分。
| 映画 | 買い物 | カラオケ | ダーツ | 合計 | |
| 男 | 22 | 15 | 38 | 25 | 100 |
| 女 | 17 | 38 | 34 | 11 | 100 |
| 合計 | 39 | 53 | 72 | 36 | 200 |
帯グラフとは?
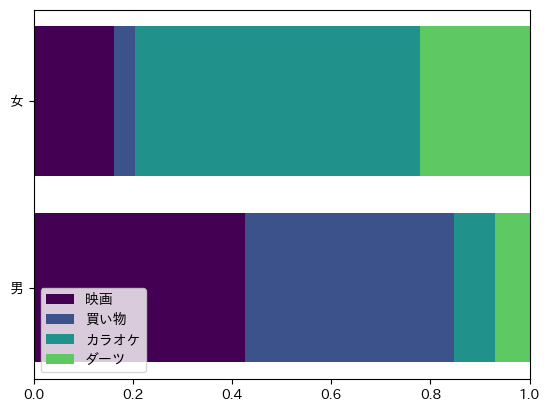
帯グラフとは、複数の項目の構成比を表すグラフです。
帯グラフは、棒グラフと同様に、各項目の長さで構成比を表しますが、棒グラフとは異なり、帯グラフは棒を横向きまたは縦向きに配置します。
これにより、帯グラフはより多くのデータを表示できるため、データの視覚化に適しています。
散布図とは?
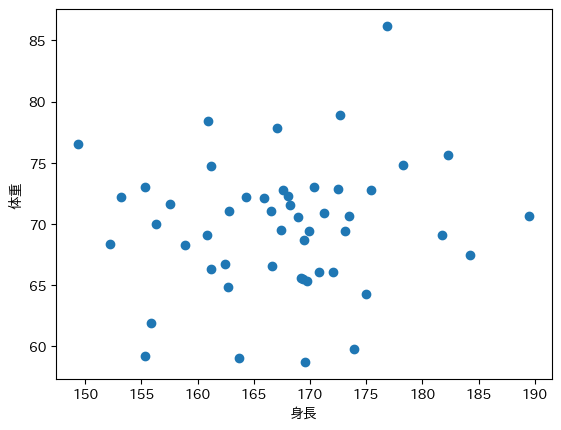
散布図は、2 つの変数間の相関を視覚化するのに役立つ統計図です。
散布図は、2 つの変数をそれぞれ X 軸と Y 軸にプロットし、各データポイントを点としてプロットすることで作成されます。点の分布は、2 つの変数間の相関を示すことができます。
たとえば、上記の図の様に身長と体重の散布図は、身長が高い人が体重も高い傾向があることを示している可能性があります。
これは、身長と体重の間に正の相関があることを示しています。
相関の方向は、点の群れがどの方向を向いているかによって示されます。点の群れが上向きになっている場合、相関は正です。点の群れが下向きになっている場合、相関は負です。
練習問題
棒グラフの練習問題
| 職種 | 平均給与 |
| 営業 | 34 |
| 技術 | 30 |
| 事務 | 26 |
| 製造 | 28 |
| 人事 | 24 |
①
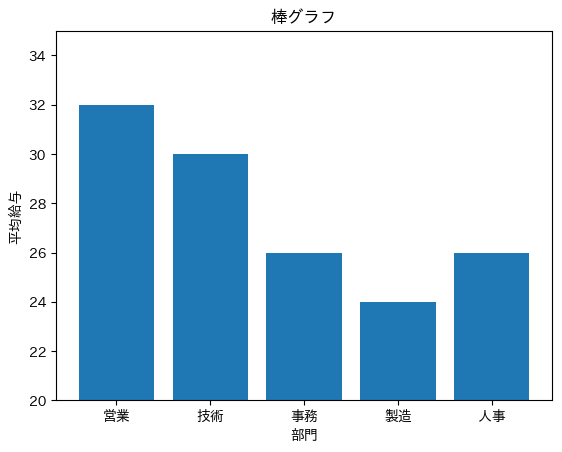
②
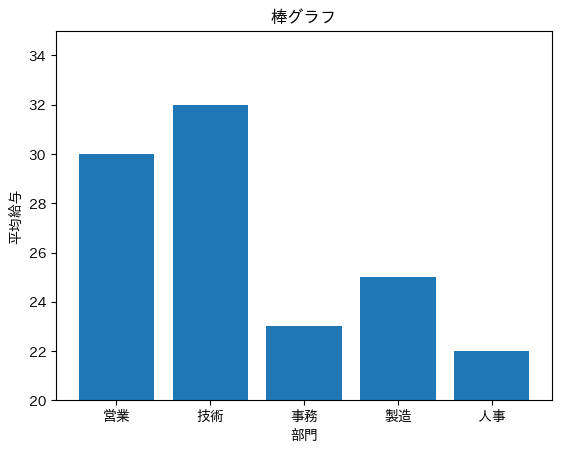
③
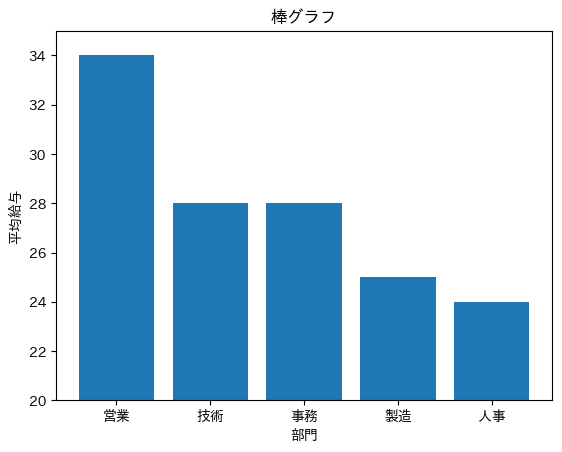
④
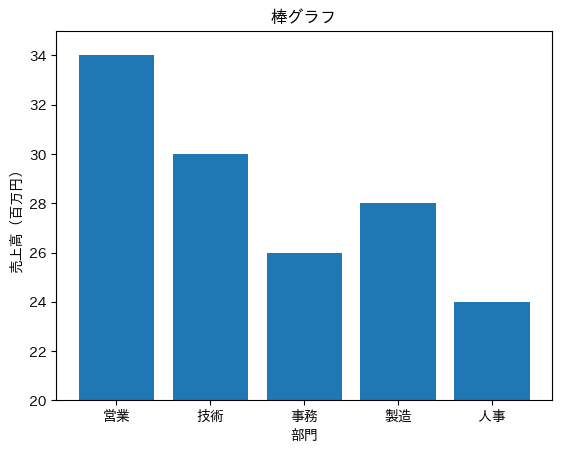
答え:④
クロス集計表の練習問題
ある企業の男女別に、会社への満足度調査を行った結果が以下の通りである。
| 非常に満足 | 満足 | 普通 | 不満 | 非常に不満 | 合計 | |
| 男 | 12 | 20 | 10 | 6 | 7 | 55 |
| 女 | 4 | 16 | 12 | 6 | 10 | 48 |
| 合計 | 16 | 36 | 22 | 12 | 17 | 103 |
この表からどのような事が読み取れるか?
- 男女ともに差は見られない
- 男の方が満足度が高い
- 女の方が満足度が高い
答え:②
「非常に満足」「満足」と答えた割合が男は$\frac{32}{55}=0.58$で、
女の場合は$\frac{20}{48}=0.416%$のため、②が正解。
散布図の練習問題
数学と国語の50人分のテスト結果から散布図を作ったのが以下の3つである。
①
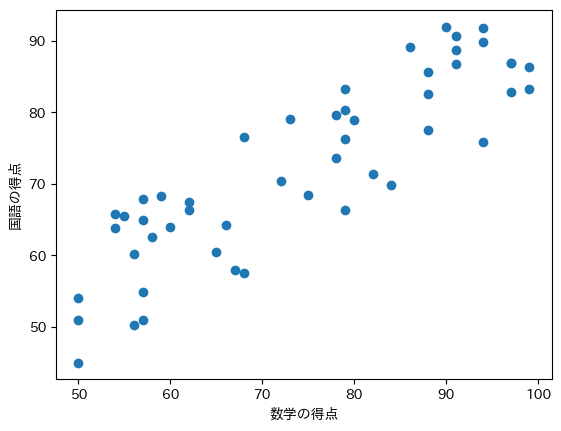
②
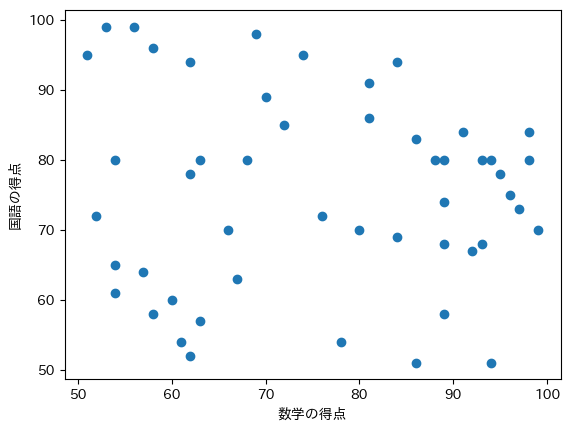
③
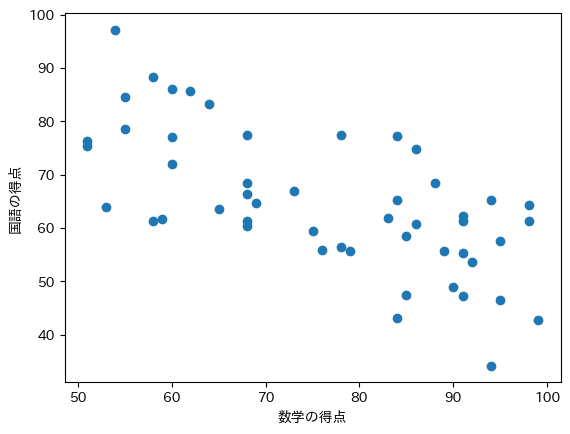
答え:①
右上がりに分布するのが正の相関の特徴なため、①が正解です。
②は均等に散らばっているため、相関が見られません。
③は右下がりですので負の相関が見られます。

Work illustrations by Storyset













