この講座の対象者は以下の方を想定しています。
- 数学は中学レベルしか分からないけど統計検定2級に合格したい
- どの参考書を見ても数式だらけで理解できない
- 確率ってどうやって求めるの?
この講座では特に、0の状態から統計検定2級に合格したいって方のために、分かりやすさをモットーに解説していきます。
今回の講座では統計で非常に重要になってくる確率の基本について解説します。
確率でつまずいてしまうと、この後に出てくる検定や回帰分析を理解する事ができませんので、確実に押さえていきましょう。
確率の考え方
皆さんも、今までにある程度確率について学んできていると思いますので、簡単に復習から始めましょう。
まず確率とは、物事の「起こりやすさ」を数値で表したものです。
取る値の範囲としては0~1の間を取り、0は「絶対に起こらない」を意味し、1は「絶対に起こる」を意味しています。
つまり1に近づくほど起こる可能性が高くなるのです。
サイコロの確率
サイコロで1が出る確率はいくつですか?と聞かれたら皆さん$\frac{1}{6}$とすぐに分かるでしょう。
では「5以上が出る確率」はどうでしょう?
これも比較的簡単ですね!
分子は5以上のサイコロの目の数。つまり$5$と$6$。
$\frac{2}{6} = \frac{1}{3}$
分母はサイコロの全ての目の数の6。
この様に、求める事ができます。
まず覚えて欲しい専門用語として↓があります。
- 試行:起こりうる結果がいくつかあり、そのどれか1つが偶然に起こる流れのこと。今回はサイコロを振る行為。
- 標本空間:試行結果全体の集合のこと。今回はサイコロを振って出る可能性があるすべての目のこと。(1~6)
- 事象:試行によって起こり得る結果をいくつか集めた集合のこと。今回は「サイコロの目が5以上になる」が事象。
同様に確からしい
また、統計の表現として「同様に確からしい」という表現が出てくる事もあります。
同様に確からしいを簡単に説明すると、サイコロの目の出方に偏りがないという意味です。
もし、サイコロがいびつな形をしており、1のでる確率が極端に低い場合などは、「同様に確からしい」とは言えません。
全ての目が出る確率が同じ場合に、言える事なのです。
そして、「同様に確からしい」と何が嬉しいのかというと、↓の公式が使えるのです。
$P(E)=\frac{事象(E)に含まれる要素の数}{標本空間(U)に含まれる要素の数}$
$P(E)$は事象Eが起こる確率を示しており、$U$は標本空間を表しています。
特に難しい事はないですね、先ほどやった事と一緒です。
分子は事象なので「偶数が出る確率」や「5以上の出る確率」などの部分です。
分母は標本空間なので、サイコロの場合は出る可能性がある全ての目の事で、6ですね!
例えば、偶数が出る確率を表すとしたら↓になります。(サイコロに含まれる偶数は3ですね。)
$P(E)=\frac{3}{6}=\frac{1}{2}$
「かつ」における確率の求め方
また、難しい日本語表現として「かつ」と「または」が出てきます。
統計は読解の学問でもあるんです(嘘ww)
エクセルやpythonなどで関数を扱った事がある人は知っていると思いますが、ANDやOR条件のやつです。
「かつ」とは何か?
これは「AかつBが起こる確率」の様に表現されます。
サイコロの場合ですと、「偶数かつ4以上」などがそれにあたります。
複数の条件に対して、それらを全て満たす場合の確率の事です。
- 偶数・・・$[2, 4, 6]$
- 4以上・・・$[4, 5, 6]$
このように、それぞれの条件を満たす事象が分かりました。
そして大事なのは、この2つの条件を両方とも満たすものが何なのか?という事です。
この場合ですと、偶数かつ4以上の物は$[4, 6]$だけになりますね。
図で表すと↓のようになります。
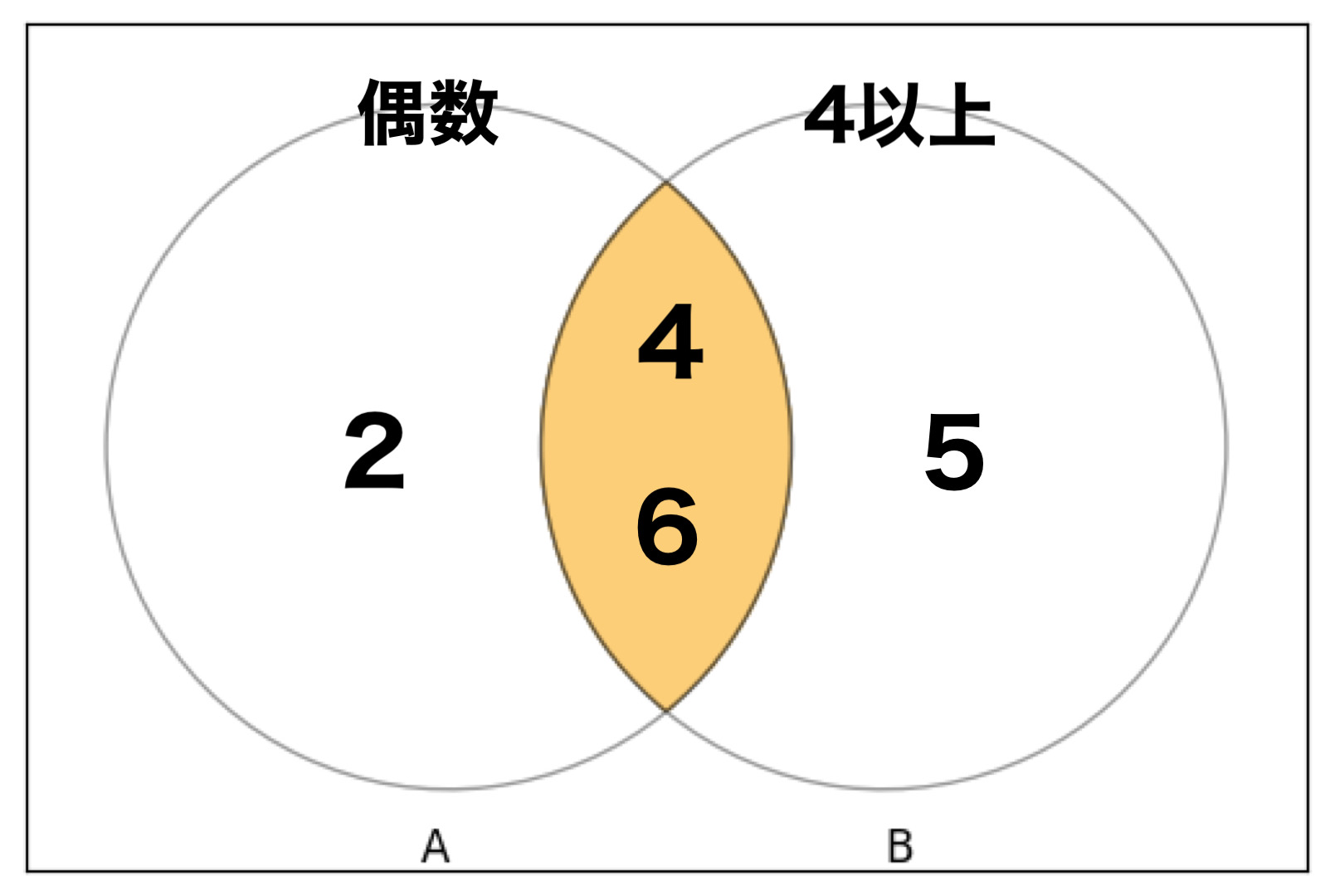
これはベン図と言い、確率の条件を表す場合によく使われます。
2つの丸がそれぞれの条件で、重なり合うオレンジの部分が偶数かつ4以上の部分です。
ちなみに条件外の$[1, 3]$に関しては、丸の外側にあるイメージです。
この様な場合、事象Aと事象Bの積事象と言いますので、覚えておきましょう。
ちなみに問題文で、「AかつB」あるいは「$A \cap B$」と書かれます。
したがって、サイコロの目が「偶数」かつ「4以上」になる確率は、↓になります。
$P(A \cap B)= \frac{A \cap Bの要素数}{標本空間の要素数}=\frac{2}{6}=\frac{1}{3}$
「または」における確率の求め方
つづいて、OR条件にあたる「または」の場合を見ていきましょう。
「または」とは何か?
これは「AまたはBが起こる確率」の様に表現されます。
サイコロの場合ですと、「奇数または2以下」などがそれにあたります。
- 偶数・・・$[1, 3, 5]$
- 2以下・・・$[1, 2]$
「かつ」とは違い、どちらかの条件に当てはまれば良いので、サイコロの「奇数または2以下」の場合は$[1, 2, 3, 5]$が答えになります。
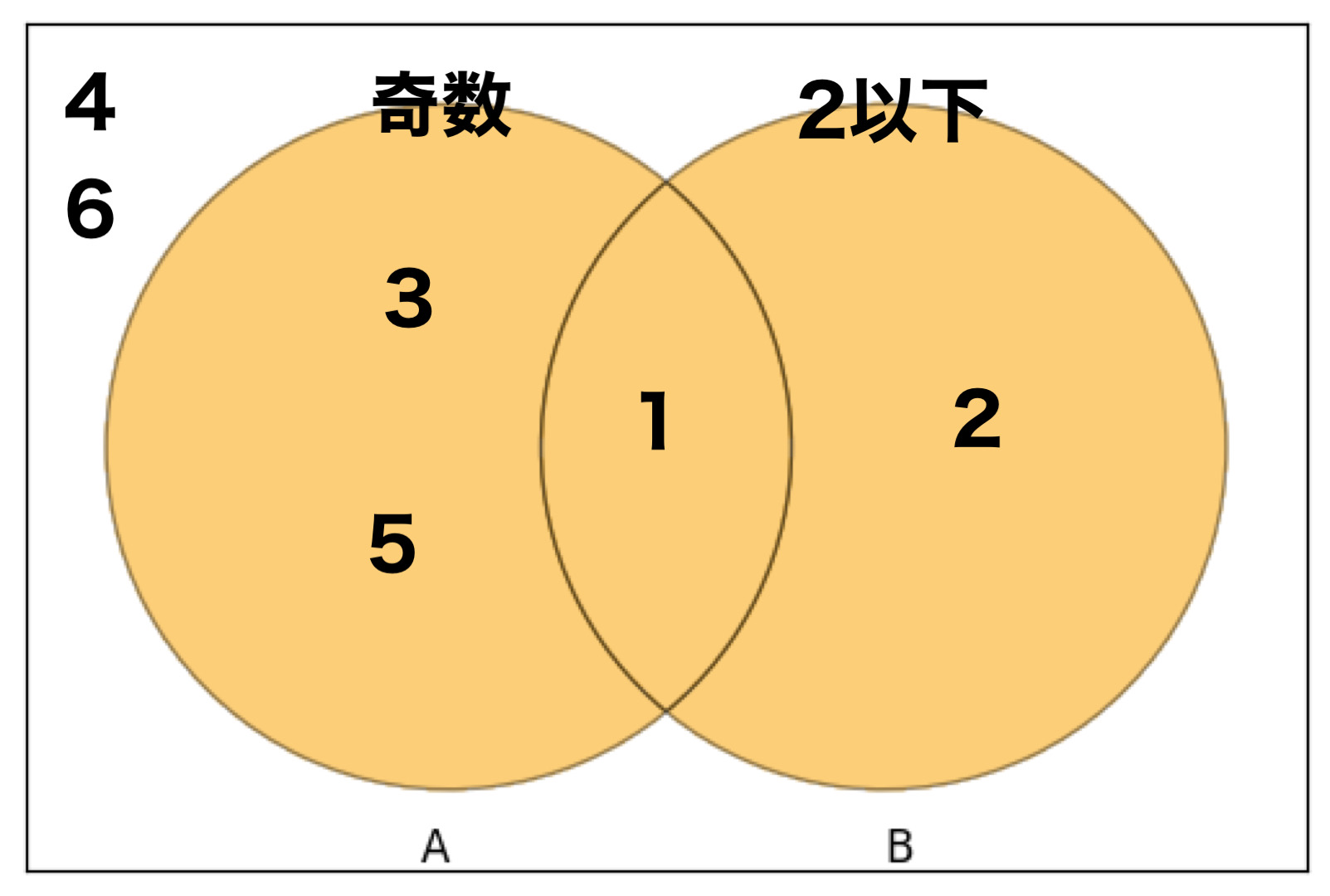
今回は2つの丸全てがオレンジになります。奇数かつ2以下の重なりあっている1ももちろん対象になります。
逆にAとBの条件から外れる$[4, 6]$は対象外になります。
この様な場合、事象Aと事象Bの和事象と言い、「AまたはB」は「$A \cup B$」で表されます。
和事象の求め方
サイコロの「奇数または2以下」の和事象の求め方は↓です。
$P(A \cup B)= \frac{A \cup Bの要素数}{標本空間の要素数}=\frac{4}{6}=\frac{2}{3}$
この時注意して欲しいのが、「$A \cup B$の要素数」の求め方です。
求めるには↓の様にします。
$A \cup B$の要素数= $A$の要素数$+B$の要素数$-A \cap B$の要素数
なぜ、$A \cap B$(AかつB)の要素数を引かないといけないかと言うと、A(奇数)の要素数[1, 3, 5]とB(2以下)の要素数[1, 2]を単純に足すと、重複している部分、つまり今回は1を二回要素としてカウントしてしまいます。
先ほどの公式の分子の部分が5になってしまうのです。
それを正すために、「AかつB」の要素数、今回は1つを引いて4とするのです。
確率の加法定理とは?
次は確率の加法定理を覚えましょう!
これを理解しないと今後の確率問題が分からなくなるので、しっかり押さえておきましょう。簡単に説明すると↓です。
確率の加法定理は、2つの排反事象のうち少なくとも1つが起こる確率を求めるためのものです。
事象Aと事象Bが排反事象である場合、AまたはBが起こる確率は、Aが起こる確率とBが起こる確率の合計に等しくなります。
イマイチピンとこないですよね?
そもそも排反が分からないと思います。
排反とは?
排反とは「AかつB」が無い状態の事を言います。
例えば、事象Aを「サイコロ目が2以下」で、事象Bを「5以上」とすると、「AかつB」な数字はないですよね?
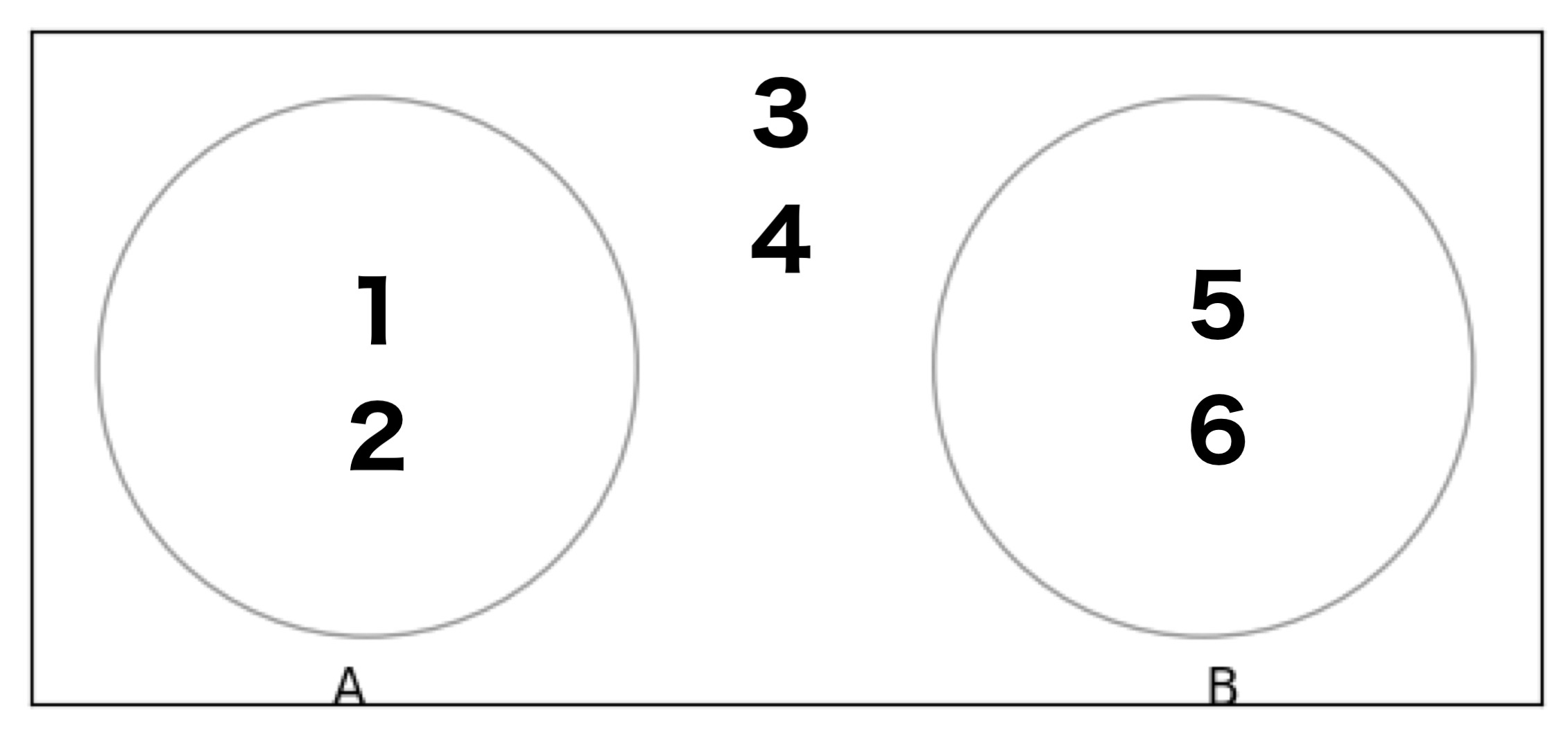
この様な状態を排反といいます。
確率の加法定理の公式
確率の加法定理の公式は↓です。
これは排反の場合に成り立ちます。
$A \cup B = P(A) + P(B)$
それぞれを解説すると、
- $A \cup B$:AまたはBが起こる確率です。
- $P(A)$:Aが起こる確率です。今回は$\frac{1}{3}$です。
- $P(B)$:Bが起こる確率です。今回は$\frac{1}{3}$です。
です。つまり、
事象AとBが排反である時、$P(A)+P(B)$をすると、$A \cup B$を求める事が出来るのです。
事象Aを「サイコロ目が2以下」で、事象Bを「5以上」とすると、これらは排反のため確率の加法定理を使い、
$P(A) + P(B) = \frac{1}{3} + \frac{1}{3} = \frac{2}{3}$
と求める事ができます。
確率の基本的性質
最後に確率の性質を覚えておきましょう!
確率は0から1の値を取る
復習ですが、確率は0から1の間の値を取ります。
マイナスになったり、1以上になったりする事はありません。
もし、そのような値を取ってしまったら計算がどこか間違っています。
空事象が起こる確率は0
例えば、「サイコロの目で7がでる確率を求めなさい」と言われても、そもそも7が無いので、確率は0になります。
この様に、要素数が0の事を空事象(くうじしょう)と言います。
空事象を表す記号は$\varnothing$です。
余事象の確率
余事象とは、ある事象の起こらない事象です。
余事象は、その事象の補集合として表すことができます。たとえば、サイコロを振って偶数の目を出す事象の余事象は、奇数の目を出す事象です。
Aの余事象は$\overline{A}$で表され、以下の式で求められます。
$P(\overline{A})=1-P(A)$
練習問題
「かつ」の練習問題
答え:$\frac{1}{13}$
「ハート」を事象A、「10以上」を事象Bとすると、A,B両方を満たすのはハートの[10, 11, 12, 13]の4枚だけですので、以下の式で求められます。
$P(A \cap B) = \frac{4}{52} = \frac{1}{13} $
「または」の練習問題
答え:$\frac{11}{26}$
事象Aを「ダイヤ」、事象Bを「3以下」とおきます。
和事象を求める時は↓の公式を使うんでしたね。
$P(A \cup B)= \frac{A \cup Bの要素数}{標本空間の要素数}$
まず$A \cup B$(AまたはB)の要素数を求めます。
$A$の要素数足す$B$の要素数から$A \cap B$(AかつB)の要素数を引けば良いんですね。
$13$(ダイヤのカード枚数)$+12$(ダイヤ、ハート、クラブ、スペードの3以下の枚数)$-3$(ダイヤかつ3以下の枚数)$=22$
これを基に公式に当てはめます。
$P(A \cup B)= \frac{22}{52}=\frac{11}{26}$














